cho hình chóp S.ABCD có đáy là hình vuông SA vuông góc (ABCD). gọi M là hình chiếu vuông góc của A lên cạnh SB cmr: a, CB vuông góc (SAB) b, AM vuông góc (SBC)
Bài 3: Đường thẳng vuông góc với mặt phẳng
a: CB vuông góc SA
CB vuông góc AB
=>CB vuông góc (SAB)
b: CB vuông góc (SAB)
=>CB vuông góc AM
mà AM vuông góc SB
nên AM vuông góc (SBC)
Đúng 1
Bình luận (0)
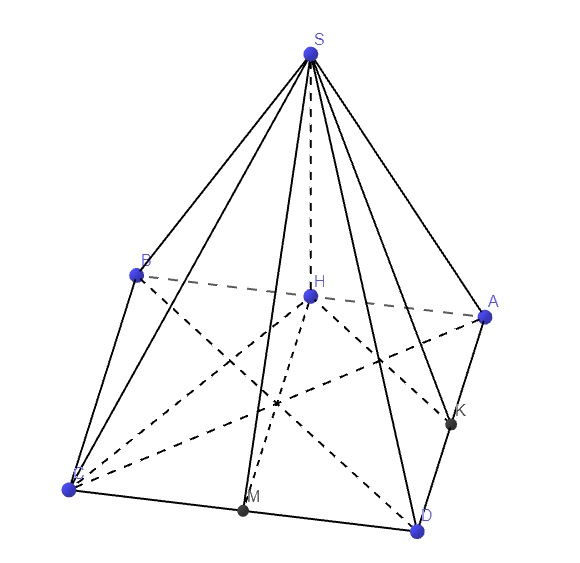
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB là tam giác đều , SC =a căn 2. Gọi H là trung điểm AB
a) CM : BC vuông (SAB) và SH vuông (ABCD)
b) Gọi M là trung điểm CD , α là góc giữa đt SM và (ABCD) . Xác định α và tính tan α
c) Gọi K là trung điểm AD . CM AC vuông SK
a.
Do tam giác SAB đều \(\Rightarrow SB=AB=a\)
Trong tam giác SBC ta có:
\(SB^2+BC^2=2a^2=SC^2\)
\(\Rightarrow\Delta SBC\) vuông tại B (pitago đảo)
\(\Rightarrow BC\perp SB\)
Mà \(BC\perp AB\left(gt\right)\)
\(\Rightarrow BC\perp\left(SAB\right)\)
Do \(SH\in\left(SAB\right)\Rightarrow BC\perp SH\) (1)
Lại có SAB là tam giác đều, mà SH là đường trung tuyến (H là trung điểm AB)
\(\Rightarrow SH\) đồng thời là đường cao hay \(SH\perp AB\) (2)
(1);(2) \(\Rightarrow SH\perp\left(ABCD\right)\)
b.
\(SH\perp\left(ABCD\right)\Rightarrow\) HM là hình chiếu vuông góc của SM lên (ABCD)
\(\Rightarrow\widehat{SMH}\) là góc giữa SM và (ABCD) hay \(\alpha=\widehat{SMH}\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
\(HM=BC=a\) \(\Rightarrow tan\alpha=\dfrac{SH}{HM}=\dfrac{\sqrt{3}}{2}\)
c.
Do H là trung điểm AB, K là trung điểm AD \(\Rightarrow\) HK là đường trung bình tam giác ABD
\(\Rightarrow HK||BD\)
Mà \(BD\perp AC\) (hai đường chéo hình vuông)
\(\Rightarrow HK\perp AC\) (3)
Lại có \(SH\perp\left(ABCD\right)\Rightarrow SH\perp AC\) (4)
(3);(4) \(\Rightarrow AC\perp\left(SHK\right)\Rightarrow AC\perp SK\)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AB=BC=a . Cạnh bên SA vuông góc với mặt phẳng đáy, SA =a căn 2
a) CM BC vuông SB
b) Xác định và tính góc giữa SC và (ABC)
a.
Do \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp SB\)
b.
\(SA\perp\left(ABC\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABC)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABC)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)
Đúng 1
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình thôi ABCD, góc \(\widehat{BAD}\) = 60 độ, cạnh SA vuông với mp đáy, SA=AB=a
a. CMR: BD vuông góc với mp(SAC)
b. Gọi H là trực tâm của tam giác SBD, M là trung điểm AD. Tính cosin của góc giữa (SB; (BHM)).
giúp mk câu b vs, mk ko bt vẽ trực tâm, cảm ơn
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A,AB=a√3 , cạnh bên SA vuông góc với mặt đáy , SA = a√3/2 , M là trung điểm của BC. a. Chứng minh BC vuông góc với (SAM) B. Tính góc giữa đường thẳng SM và mặt phẳng (ABC)
a: BC vuông góc AM
BC vuông góc SA
=>BC vuông góc (SAM)
b: BC vuông góc (SAM)
=>BC vuông góc SM
=>(SM;(ABC))=90 độ
Đúng 1
Bình luận (0)
cho hình chóp SABCD đều
a. CM: SO vuông góc đáy ( O giao của 2 đường chéo)
b. tính góc tạo bởi cạnh bên và mặt phẳng đáy
a: Vì đây là hình chóp đều
nên đường thẳng nối từ đỉnh đến tâm của đáy sẽ vuông góc với đáy
=>SO vuông góc (ABCD)
b: (SA;ABCD)=(AS;AO)=góc SAO
(SB;ABCD)=(BS;BO)=góc SBO
(SC;ABCD)=(CS;CO)=góc SCO
(SD;ABCD)=(DS;DO)=góc SDO
Đúng 0
Bình luận (0)
a: BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
MN vuông góc SO
MN//BD(SM/SB=SN/SD)
=>MN vuông góc AC
=>MN vuông góc (SAC)
=>(SAC) vuông góc (CMN)
b: SB vuông góc AM; SB vuông góc CM
=>SB vuông góc (MAC)
=>(SBD) vuông góc (MAC)
AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SDB)
=>(ABCD) vuông góc (SBD)
=>((MAC);(ABCD))=góc SBD=60+45=105 độ
Đúng 0
Bình luận (0)
Mệnh đề nào sau đây có thể sai?A. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song songB. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song songC. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song songD. Một đường thẳng và một mặt phẳng (không chứa đường thẳng đã cho) cùng vuông góc với một đường thẳng thì song song nhau
Đọc tiếp
Mệnh đề nào sau đây có thể sai?
A. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song
B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song
D. Một đường thẳng và một mặt phẳng (không chứa đường thẳng đã cho) cùng vuông góc với một đường thẳng thì song song nhau
Trong không gian cho đường thẳng Δ và điểm O. Qua O có mấy đường thẳng vuông góc với Δ cho trước?
A. 1
B. 2
C. 3
D. Vô số
Cho 2 đường thẳng phân biệt a,b với mặt phẳng P, trong đó a ⊥ P. Mệnh đề nào sau đây là sai?
A. Nếu b ⊥ P thì b // a
B. Nếu b // P thì b ⊥ a
C. Nếu b // a thì b ⊥ P
D. Nếu b ⊥ a thì b // P