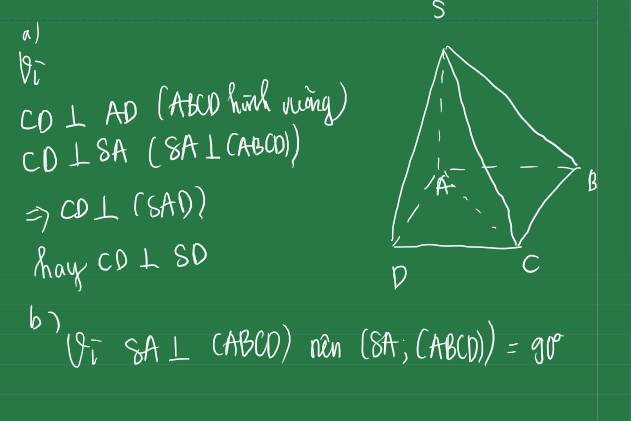Cho hình chóp S.ABCD có ABCD là hình vuông, SA vuông góc với ABCD a) Chúng minh CD vuông góc SD b) Xác định góc tạo bởi SA và (ABCD)
Bài 3: Đường thẳng vuông góc với mặt phẳng
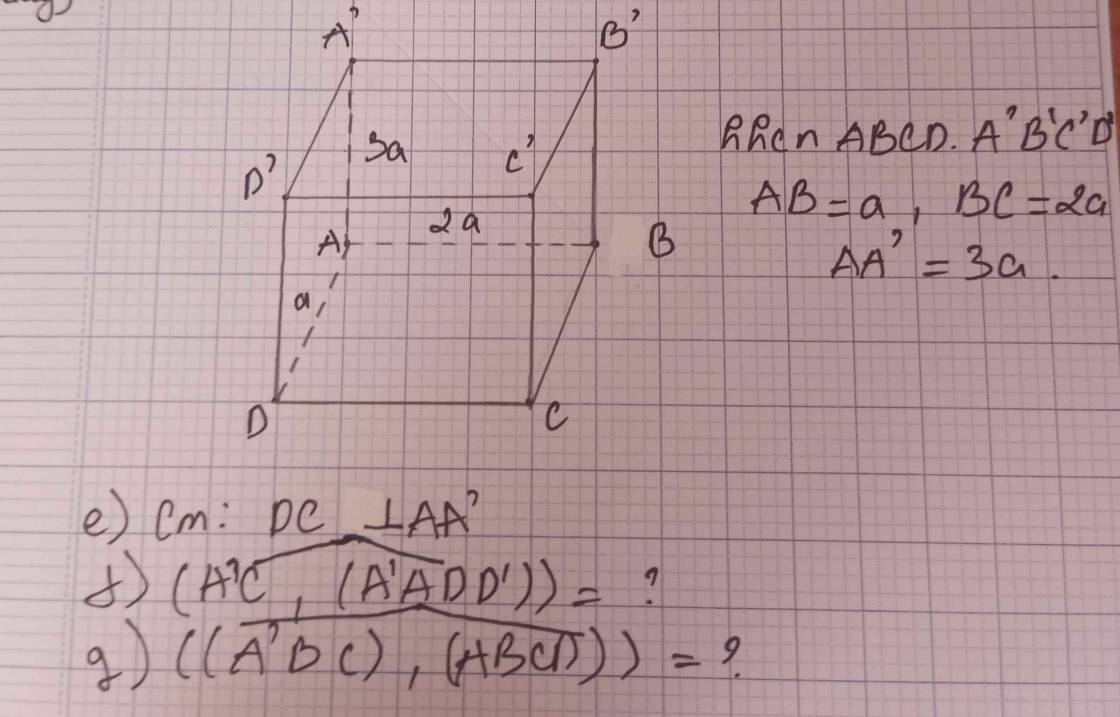
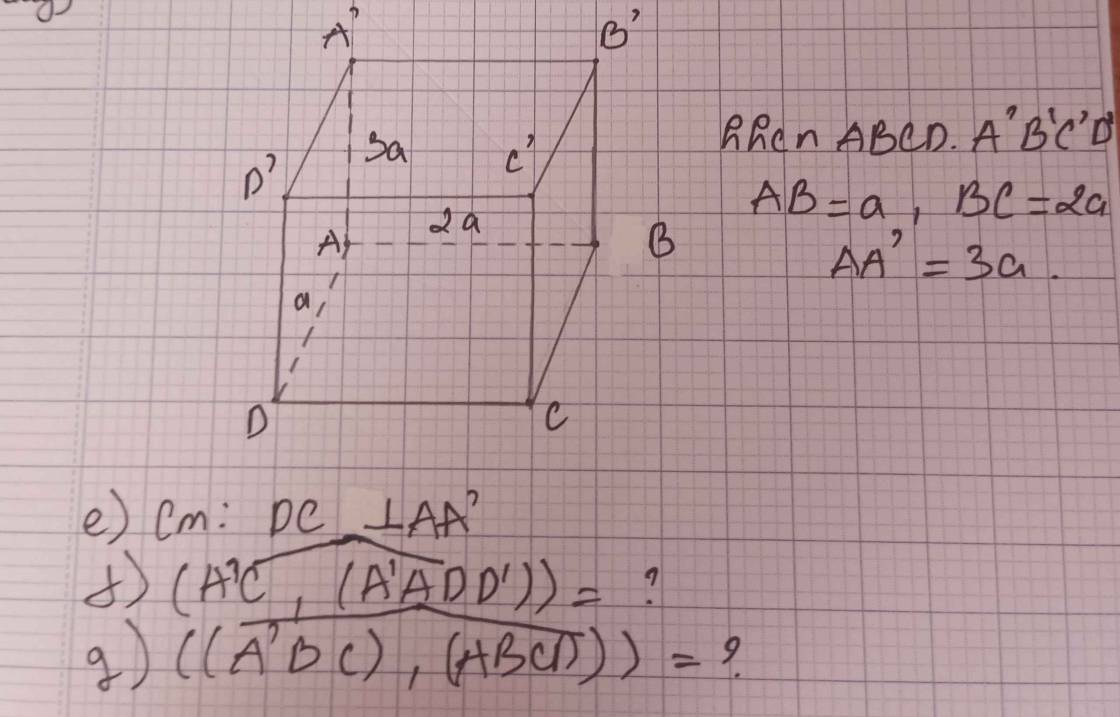
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, tìm hình chiếu của: a) Tìm hình chiếu của SA trên các mặt phẳng (SBC) và (SCD) b) Tìm hình chiếu của SC trên các mp (SAB) (SAD) c) Tìm hình chiếu của AB trên mp (SCD)
a: AB vuông góc BC tại B
=>Hình chiếu của SA lên (SBC) là SB
AD vuông góc DC tại D
=>Hình chiếu của SA lên (SDC) là SD
b: CB vuông góc AB tại B
=>Hình chiếu của SC trên (SAB) là SB
CD vuông góc AD tại D
=>Hình chiếu của SC lên (SAD) là SD
Đúng 1
Bình luận (0)
giúp tớ vssss

Câu 1:
BC vuông góc SA
BC vuông góc BA
=>BC vuông góc (SAB)
=>BC vuông góc SB
=>ΔSBC vuông tại B
CD vuông góc SA
DC vuông góc AD
=>DC vuông góc (SAD)
=>DC vuông góc SD
=>ΔDCS vuông tại D
Câu 2:
CD vuông góc (SAD)
AH vuông góc (SAD)
=>CD vuông góc AH
mà AH vuông góc SD
nên AH vuông góc (SCD)
=>AH vuông góc SC
Đúng 0
Bình luận (0)
Cho hình chóp SABC, đáy tam giác ABC vuông tại B. Gọi H là hình chiếu của A lên SB(SA vuông góc (ABC)) a. Chứng minh: BC vuông góc (SAB) B. Gọi I là hình chiếu của B lên AC Chứng minh BI vuông góc (SAC) c. Kẻ AK vuông góc SC tại K, Chứng minh:AH vuông góc SC
a: BC vuông góc SA
BC vuôg góc AB
=>BC vuông góc (SAB)
b: BI vuông góc SA
BI vuông góc AC
=>BI vuông góc (SAC)
Đúng 0
Bình luận (0)
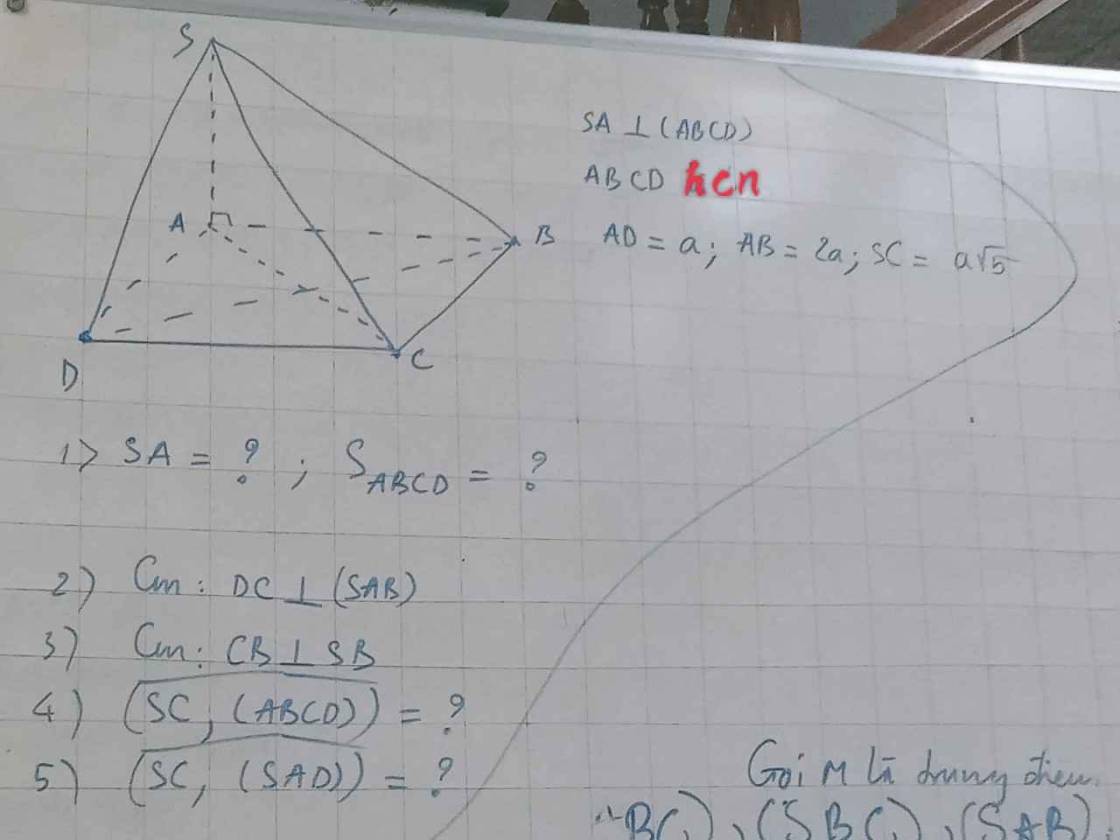
Cho hình chóp SABCD, ABCD là hình chữ nhật với AB=a, BC=a√3. Kẻ BK vuông góc SC. a, chứng minh rằng SC vuông góc AK B, Cho SB=2a. Tính góc giữa SD và mặt ABCD. c, tính góc giữa SC và mặt phẳng ADK
1: \(S_{ABCD}=a\cdot2a=2a^2\)
AC=căn (2a)^2+a^2=a căn 5
\(SA=\sqrt{SC^2-AC^2}=0\)
3: CB vuông góc BA
CB vuông góc SA
=>CB vuông góc (SBA)
=>CB vuông góc SB
4: \(\widehat{SC,\left(ABCD\right)}=\widehat{SC;AC}=\widehat{ACS}=0^0\)
Đúng 1
Bình luận (0)
Cho hình chóp SABC có đáy ABC là tam giác vuông tại C. Cạnh bên SA vuông góc với đáy. a)Chứng minh BC vuông góc với (SAC)? b)Gọi AH là đường cao của tam giác SAC. Chứng minh AH vuông góc với (SBC)?
a: BC vuông góc SA
BC vuông góc CA
=>BC vuông góc (SAC)
b: AH vuông góc SC
BC vuông góc (SAC)
=>BC vuông góc AH
=>AH vuông góc (SBC)
Đúng 0
Bình luận (1)
Cho hình chóp SABCD có đáy là hình vuông ABCD có SA vuông góc với AD, BD vuông góc với SC, AE vuông góc với SB, AF vuông góc với SD. Cm EF vuông góc với SAC