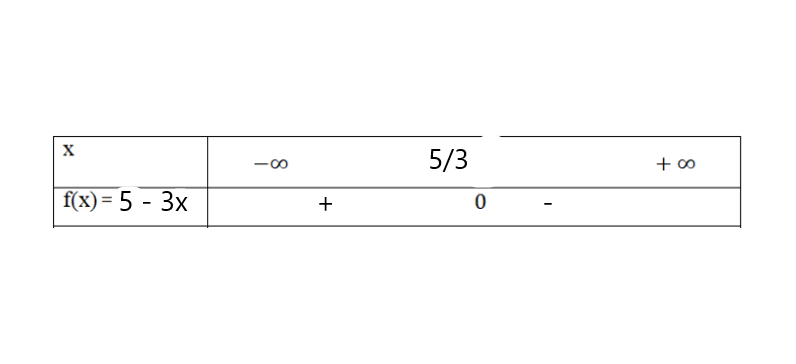cho hàm số y = x 3 − 3 x 2 2 , có đồ thị là (c). gọi m là một điểm thuộc đồ thị (c). viết phương trình tiếp tuyến của ( c) tại m, biết m cùng với hai điểm cực trị của đồ thị tạo thành một tam giác có diện tích bằng 6
Bài 3: Đạo hàm của hàm số lượng giác
Giúp e câu 3 đi mn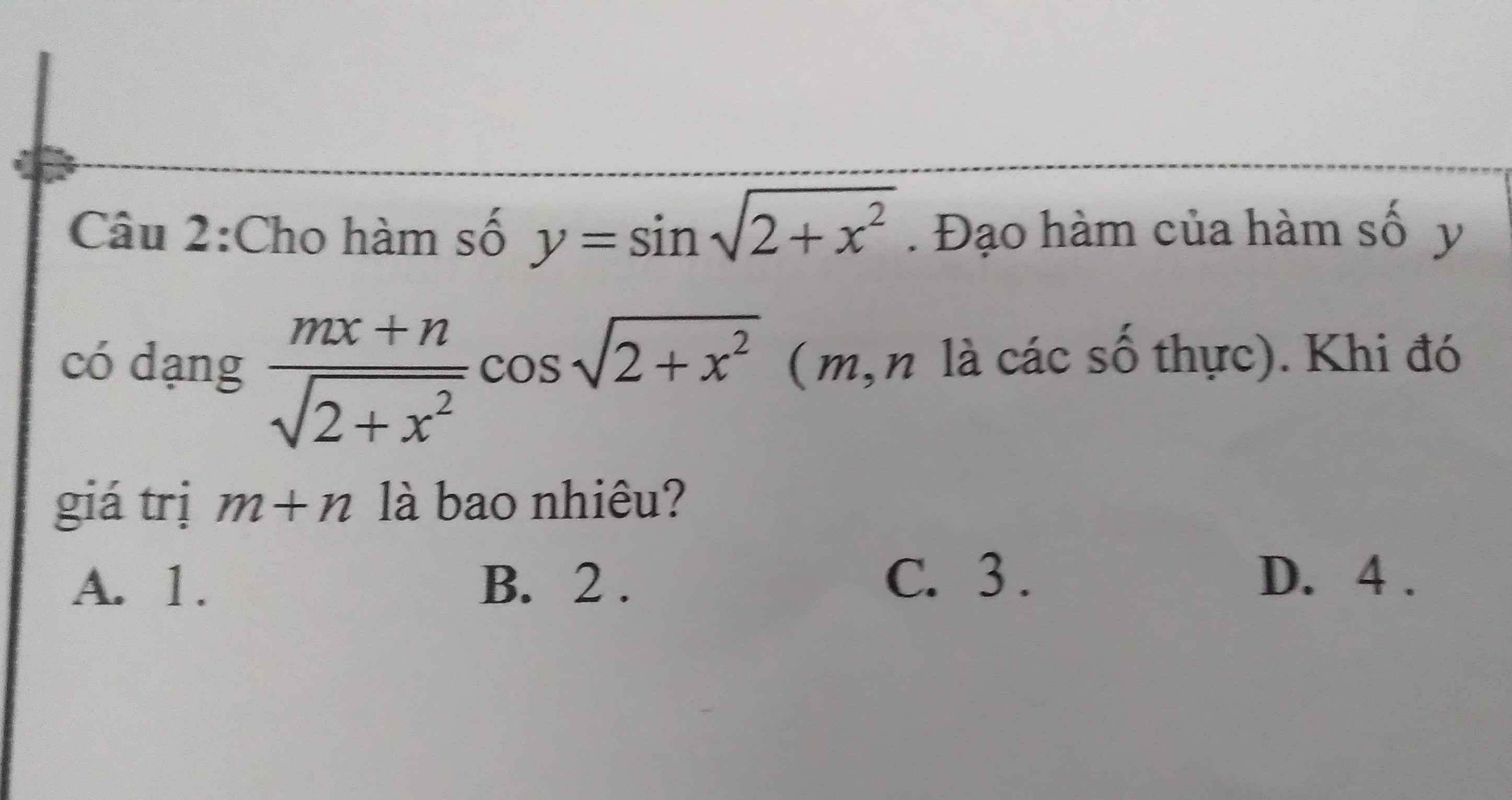
\(y'=cos\sqrt{2+x^2}.\left(\sqrt{2+x^2}\right)'=cos\sqrt{2+x^2}.\dfrac{2x}{2\sqrt{2+x^2}}\)
\(=\dfrac{x}{\sqrt{2+x^2}}.cos\sqrt{2+x^2}\)
\(\Rightarrow m=1;n=0\)
\(\Rightarrow m+n=1\)
Đúng 0
Bình luận (0)
Giúp e câu 2 ạ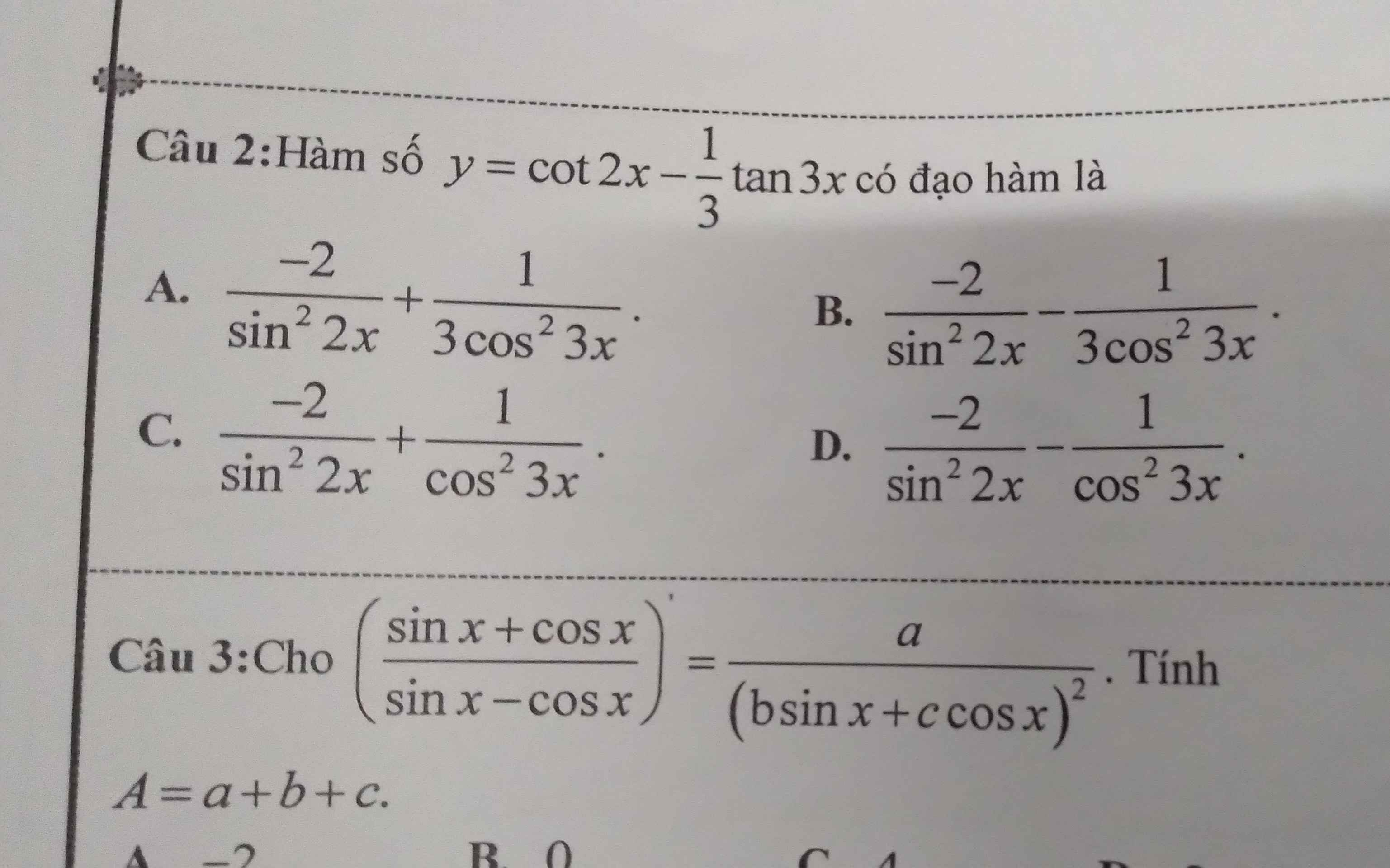
2.
\(y'=\left(cot2x\right)'-\left(\dfrac{1}{3}tan3x\right)'=-\dfrac{1}{sin^22x}.\left(2x\right)'-\dfrac{1}{3cos^23x}.\left(3x\right)'\)
\(=\dfrac{-2}{sin^22x}-\dfrac{1}{cos^23x}\)
Đúng 0
Bình luận (0)
cho hàm số f(x)=sin2x+2(1-2m)cos2x-2mx+1. Với giá trị nào của tham số m thì phương trình f'(x)=0 có nghiệm
\(f'\left(x\right)=2cos2x-4\left(1-2m\right)sin2x-2m\)
Phương trình \(f'\left(x\right)=0\) có nghiệm
\(\Leftrightarrow2cos2x-4\left(1-2m\right)sin2x=2m\) có nghiệm
\(\Leftrightarrow cos2x-2\left(1-2m\right)sin2x=m\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(1^2+4\left(1-2m\right)^2\ge m^2\)
\(\Leftrightarrow15m^2-16m+5\ge0\)
\(\Leftrightarrow15\left(m-\dfrac{8}{15}\right)^2+\dfrac{11}{15}\ge0\) (luôn đúng)
Vậy \(f'\left(x\right)=0\) có nghiệm với mọi m
Đúng 0
Bình luận (0)
1.
a)y'=2sinx.cosx-3sin3x=sin2x-3sin3x
b)y'=\(\dfrac{\left(cosx\right)'\left(2+sin2x\right)-cosx\left(2+sin2x\right)'}{\left(2+sin2x\right)^2}\)=\(\dfrac{-2sinx-sinxsin2x-2cosxcos2x}{\left(2+sin2x\right)^2}\)
Đúng 0
Bình luận (0)
2. y'=-2sin2x.sin3x+cos2x.3cos3x
y'=\(\dfrac{-2sinx}{2\sqrt{3+2cosx}}\)
Đúng 0
Bình luận (0)
Giúp em làm vd2 ạ
a.
\(y'=\left(x^2\right)'+\left(4sinx\right)'=2x+4cosx\)
b.
\(y'=\left(2x^3\right)'-\left(sinx\right)'+\left(2\right)'=6x^2-cosx\)
c.
\(y'=\left(5sin\left(x-\dfrac{\pi}{4}\right)\right)'=5cos\left(x-\dfrac{\pi}{4}\right).\left(x-\dfrac{\pi}{4}\right)'=5cos\left(x-\dfrac{\pi}{4}\right)\)
Đúng 0
Bình luận (0)
Xét dấu nhị thức f(x)=5-3x
Giá trị f ' (π/6) biết f(x)= 2cos x là
\(f'\left(x\right)=\left(2cox\right)'=2.\left(-sinx\right)=-2sinx\\ f'\left(\dfrac{\pi}{6}\right)=-2.sin\left(\dfrac{\pi}{6}\right)=-1\)
Đúng 2
Bình luận (0)
mỗi đạo hàm y=sin(π/2-2x)
\(y=\sin\left(\dfrac{\pi}{2}-2x\right)=\cos2x\Rightarrow y'=\left(\cos2x\right)'=-2\sin2x\)
Đúng 1
Bình luận (0)
Y=cot^3*3πx/2
Chắc đề là tính đạo hàm của \(y=cot^3\left(\dfrac{3\pi x}{2}\right)\)?
Nếu vậy:
\(y'=3cot^2\left(\dfrac{3\pi x}{2}\right).\left[cot\left(\dfrac{3\pi x}{2}\right)\right]'=3cot^2\left(\dfrac{3\pi x}{2}\right).\left(-\dfrac{1}{sin^2\left(\dfrac{3\pi x}{2}\right)}\right).\dfrac{3\pi}{2}\)
\(=-\dfrac{9\pi}{2}.\dfrac{cos^2\left(\dfrac{3\pi x}{2}\right)}{sin^4\left(\dfrac{3\pi x}{2}\right)}\)
Đúng 4
Bình luận (1)