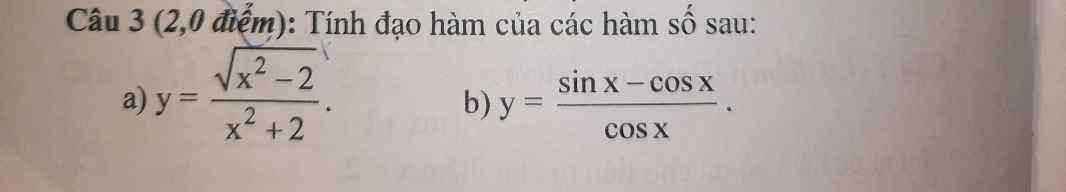a.\(y=\dfrac{\sqrt{x^2-2}}{x^2+2}\Rightarrow y'=\dfrac{\left(\sqrt{x^2-2}\right)'\left(x^2+2\right)-\left(x^2+2\right)'.\sqrt{x^2-2}}{\left(x^2+2\right)^2}\)
\(\Rightarrow y'=\dfrac{\dfrac{x}{\sqrt{x^2-2}}\left(x^2+2\right)-2x\sqrt{x^2-2}}{\left(x^2+2\right)^2}\)
\(=\dfrac{x\left(x^2+2\right)-2x\left(x^2-2\right)}{\left(x^2+2\right)^2\sqrt{x^2-2}}=\dfrac{-x^3+6x}{\left(x^2+2\right)^2\sqrt{x^2-2}}\)
b. \(y=\dfrac{sinx-cosx}{cosx}=tanx-1\Rightarrow y'=\dfrac{1}{cos^2x}\)