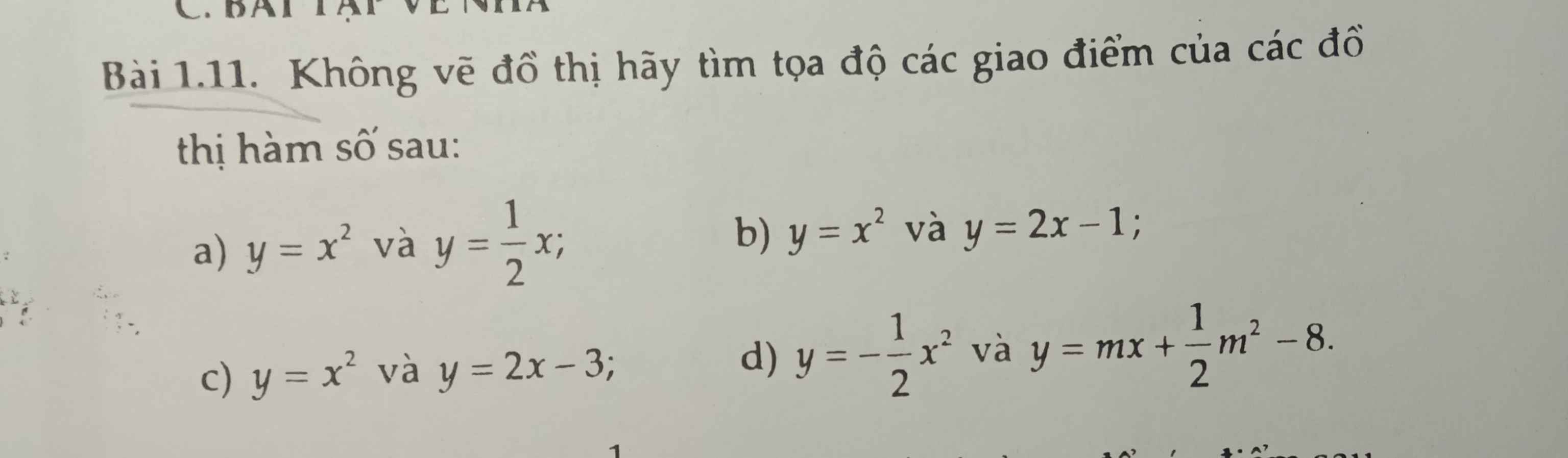giúp với ạ
Bài 1: Hàm số y = ax^2 (a khác 0)
2:
a: 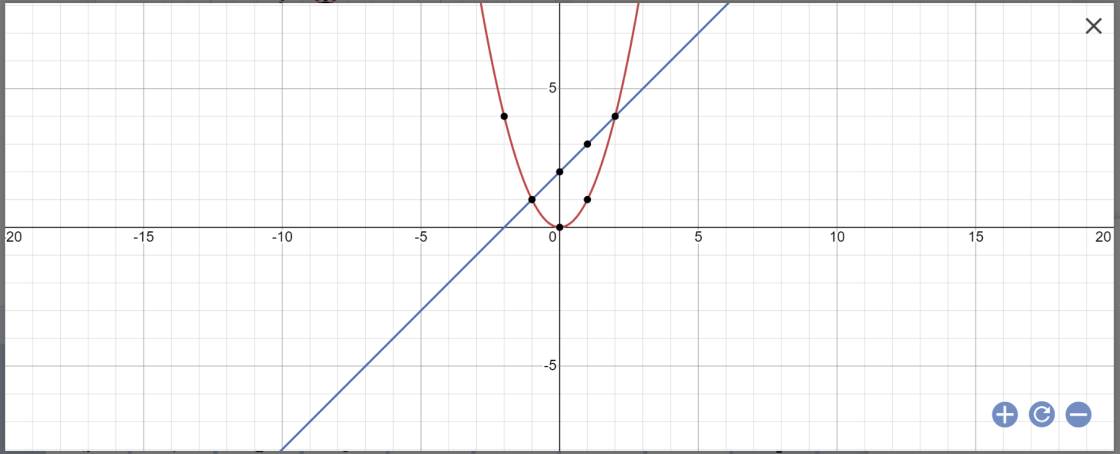
b: PTHĐGĐ là:
x^2-x-2=0
=>(x-2)(x+1)=0
=>x=2 hoặc x=-1
=>y=4 hoặc y=1
Đúng 0
Bình luận (0)
Mn giúp mình với ạ Trong mặt phẳng toạ độ có điểm M (1; -2) thuộc đồ thị hàm số y= ax². a, Tìm hệ số a. b, vẽ đồ thị hàm số vừa tìm được
a: Thay x=1 và y=-2 vào (P), ta được:
a*1^2=-2
=>a=-2
b: y=-2x^2
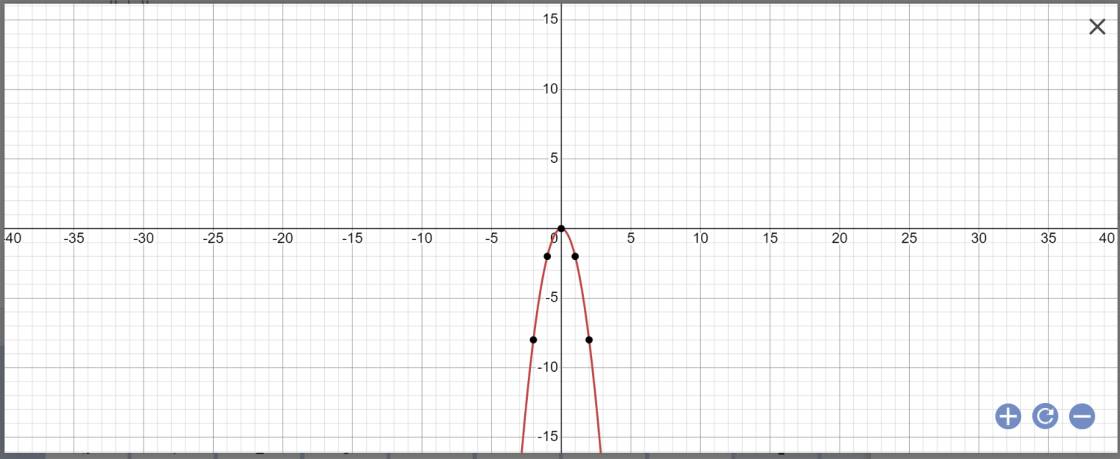
Đúng 0
Bình luận (0)
Cho parabol (P):y=x^2 và đường thẳng d:y= 2x+3
Ở thành phố St. Louis (Mỹ) có một cái cổng có dạnh hình Parabol bề lõm xuống dưới, đó là cổng Arch (Gateway Arch). Giả sử ta lập một hệ tọa độ Oxy như trên hình (x và y tính bằng mét), một chân của cổng ở vị trí A có x 81, một điểm M trên cổng có tọa độ là (– 71;– 143). a) Tìm hàm số bậc hai có đồ thị chứa cung parabol nói trên. b) Tính chiều cao OH của cổng (làm tròn đến hàng đơn vị).
Đọc tiếp
Ở thành phố St. Louis (Mỹ) có một cái cổng có dạnh hình Parabol bề lõm xuống dưới, đó là cổng Arch (Gateway Arch). Giả sử ta lập một hệ tọa độ Oxy như trên hình (x và y tính bằng mét), một chân của cổng ở vị trí A có x = 81, một điểm M trên cổng có tọa độ là (– 71;– 143). a) Tìm hàm số bậc hai có đồ thị chứa cung parabol nói trên. b) Tính chiều cao OH của cổng (làm tròn đến hàng đơn vị).
Xem thêm câu trả lời
Cho hai hàm số y = x^2 và y =- x + 2.
a) Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ
b) Tìm tọa độ giao điểm của hai đồ thị trên bằng phương pháp đại số
c) Gọi A, B là giao điểm của 2 đồ thị trên. Tính diện tích tam giác AOB
a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2-\dfrac{1}{2}x=0\\y=\dfrac{1}{2}x\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(0;0\right);\left(\dfrac{1}{2};\dfrac{1}{4}\right)\right\}\)
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2-2x+1=0\\y=x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)=\left(1;1\right)\)
c: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2-2x+3=0\\y=x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\varnothing\)
Đúng 2
Bình luận (4)
mình làm 1 câu, mấy câu sau bạn làm tương tự
a, Hoành độ giao điểm tm pt
\(x^2-\dfrac{1}{2}x=0\Leftrightarrow x\left(x-\dfrac{1}{2}\right)=0\Leftrightarrow x=0;x=\dfrac{1}{2}\)
Với x = 0 => y = 0
Với x = 1/2 => y = 1/4
Vậy (P) cắt (d) tại O(0;0) ; A(1/2;1/4)
Đúng 2
Bình luận (0)
viết phương trình đường thẳng đi qua 2 điểm A(2;-2) và B(-1;3)
Gọi \(\left(d\right):y=ax+b\) đi qua hai điểm \(A\left(2;-2\right)\) và \(B\left(-1;3\right)\)
\(\Rightarrow\left\{{}\begin{matrix}2a+b=-2\\-a+b=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{3}\\b=\dfrac{4}{3}\end{matrix}\right.\)
Vậy phương trình đường thẳng đi qua hai điểm \(A\left(2;-2\right)\) và \(B\left(-1;3\right)\) là \(y=-\dfrac{5}{3}x+\dfrac{4}{3}\).
Đúng 1
Bình luận (0)
Gọi ptđt trên có dạng (d) : y = ax + b
(d) đi qua A(2;-2) <=> 2a + b = -2 (1)
(d) đi qua B(-1;3) <=> -a + b = 3 (2)
Từ (1) ; (2) ta có hệ \(\left\{{}\begin{matrix}3a=-5\\b=3+a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{3}\\b=\dfrac{4}{3}\end{matrix}\right.\)
Vậy ptđt (d) có dạng y = -5/3x + 4/3
Đúng 1
Bình luận (0)
d cắt P: y=ax^2 tại điểm có x=-3 . d cắt Ox tại điểm có hoành độ= 4
Cho (P) y= 2x² (d) y= -2mx+m+1.
Tìm m để d cắt (P) tại 2 điểm pb x1, x2 sao cho 1/(2x1-1)² + 1/(2x2-1)² =2
Các idol toán học giúp mk vs ạ
PT hoành độ giao điểm: \(2x^2=-2mx+m+1\)
\(\Leftrightarrow2x^2+2mx-\left(m+1\right)=0\)
Vì (P) cắt (d) tại 2 điểm phân biệt nên \(\Delta'=m^2+2\left(m+1\right)>0\)
\(\Leftrightarrow\left(m+1\right)^2>0\left(\text{đúng với mọi }m\ne-1\right)\)
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{2m}{2}=-m\\x_1x_2=\dfrac{-\left(m+1\right)}{2}\end{matrix}\right.\)
Ta có \(\dfrac{1}{\left(2x_1-1\right)^2}+\dfrac{1}{\left(2x_2-1\right)^2}=2\)
\(\Leftrightarrow\dfrac{4x_2^2-4x_2+1+4x_1^2-4x_1+1}{\left[\left(2x_1-1\right)\left(2x_2-1\right)\right]^2}=2\\ \Leftrightarrow4\left[\left(x_1+x_2\right)^2-2x_1x_2\right]-4\left(x_1+x_2\right)+2=2\left[4x_1x_2-2\left(x_1+x_2\right)+1\right]^2\\ \Leftrightarrow4\left(m^2+m+1\right)+4m=2\left(-2m-2+2m+1\right)^2\\ \Leftrightarrow4m^2+4m+4+4m=2\\ \Leftrightarrow2m^2+4m+1=0\\ \Leftrightarrow\left[{}\begin{matrix}m=\dfrac{-2+\sqrt{2}}{2}\left(tm\right)\\m=\dfrac{-2-\sqrt{2}}{2}\left(tm\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)