Trong mặt phẳng tọa độ Oxy cho \(\overrightarrow{a}=2\overrightarrow{i}\) , \(\overrightarrow{b}=-3\overrightarrow{j}\), \(\overrightarrow{c}=3\overrightarrow{i}-4\overrightarrow{j}\)
Phân tích vecto c theo hai vecto a và vecto b
Trong mặt phẳng tọa độ Oxy cho \(\overrightarrow{a}=2\overrightarrow{i}\) , \(\overrightarrow{b}=-3\overrightarrow{j}\), \(\overrightarrow{c}=3\overrightarrow{i}-4\overrightarrow{j}\)
Phân tích vecto c theo hai vecto a và vecto b
Giả sử `\vec{c}=m\vec{a}+n\vec{b}`
`<=>(3;-4)=m(2;0)+n(0;-3)`
`<=>(3;-4)=(2m;-3n)`
`<=>{(m=3/2),(n=4/3):}`
`=>\vec{c}=3/2\vec{a}+4/3\vec{b}`
cho tam giác ABC có A(2;3) B(-1;-1) C(10;3) M(a,b) nằm trên BC sao cho DE có độ dài nhỏ nhất với D,E lần lượt là hình chiếu vuông góc của M lên AC,AB .tìm tọa độ M
trong M P O X Y cho A(3,-1) B ( 4,2)
a, O A B có thẳng hàng không
b, tìm M (x,y0 để O A B M là hình bình hành
c, tìm toạ độ trung điểm I cua AB
d, tìm toạ độ trọng tâm G của tam giác O A B
nhờ mọi người giúp mình với ạ
a: vect OA=(3;-1)
vecto OB=(4;2)
Vì 3/4<>-1/2
nên O,A,B ko thẳng hàng
b: OABM là hình bình hành
nên vecto OA=vecto MB
=>4-x=3 và 2-y=-1
=>x=1 và y=3
c: Tọa độ I là:
x=(3+4)/2=3,5 và y=(-1+2)/2=0,5
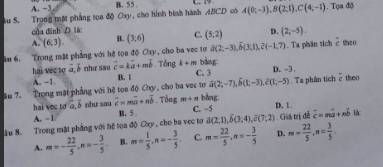
giải ra giúp mk vs cảm ơn ạ
Câu 5:
ABCD là hình bình hành
=>vecto AB=vecto DC
=>\(\left\{{}\begin{matrix}4-x=2-0=2\\-1-y=1+3=4\end{matrix}\right.\Leftrightarrow D\left(2;-5\right)\)
Câu 6:
vecto c=k*vecto a+m*vecto b
=>\(\left\{{}\begin{matrix}-1=2k+3m\\7=-3k+m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}k=-2\\m=1\end{matrix}\right.\)
=>k+m=-1
Câu 7: B
Câu 8: C
(1) trong mặt phẳng tọa độ Oxy, cho hai vecto \(\overrightarrow{a}=\left(1;-4\right)\), \(\overrightarrow{b}=\left(0;2\right)\). tọa độ của vecto \(\overrightarrow{u}=2\overrightarrow{a}-\overrightarrow{b}\) là?
(2) trong mặt phẳng tọa độ Oxy, cho hai vecto \(\overrightarrow{a}=\left(-7;3\right)\), \(\overrightarrow{b}=\left(4;1\right)\). tọa độ của vecto \(\overrightarrow{u}=\overrightarrow{b}-2\overrightarrow{a}\) là?
(3) trong mặt phẳng tọa độ Oxy, cho hai vecto \(\overrightarrow{u}=\left(-5;4\right)\), \(\overrightarrow{v}=-3\overrightarrow{j}\). tọa độ của vecto \(\overrightarrow{a}=2\overrightarrow{u}-5\overrightarrow{v}\) là?
(4) trong mặt phẳng tọa độ Oxy, cho hai điểm A (1;1), B (4;-7) và \(\overrightarrow{OM}=2\overrightarrow{OA}-5\overrightarrow{OB}\). tổng hoành độ và tung độ của điểm M là?
giúp mk vs ạ mk cần gấp thank
(1); vecto u=2*vecto a-vecto b
=>\(\left\{{}\begin{matrix}x=2\cdot1-0=2\\y=2\cdot\left(-4\right)-2=-10\end{matrix}\right.\)
(2): vecto u=-2*vecto a+vecto b
=>\(\left\{{}\begin{matrix}x=-2\cdot\left(-7\right)+4=18\\y=-2\cdot3+1=-5\end{matrix}\right.\)
(3): vecto a=2*vecto u-5*vecto v
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\cdot\left(-5\right)-5\cdot0=-10\\b=2\cdot4-5\cdot\left(-3\right)=15+8=23\end{matrix}\right.\)
(4): vecto OM=(x;y)
2 vecto OA-5 vecto OB=(-18;37)
=>x=-18; y=37
=>x+y=19
Cho 2 điểm A(4;4), B(0;1). Tìm điểm C trên Oy sao cho trung trực của đoạn AC đi qua B.
C thuộc Oy nên C(0;y)
B nằm trên trung trực của AC nên BA=BC
=>BA^2=BC^2
=>(4-0)^2+(1-4)^2=(0-0)^2+(y-1)^2
=>(y-1)^2=4^2+3^2=25
=>y-1=5 hoặc y-1=-5
=>y=6 hoặc y=-4
Cho M(4,1) và 2 điểm A(a,0)và B(0,b) với a,b>0 sao cho A,B,M thẳng hàng.Xác định tọa độ A,B sao cho
a, Diện tích tam giác OAB nhỏ nhất
b, OA+OB nhỏ nhất
c, nhỏ nhất
Trong Oxy cho A(2;1), B(3;3)
a. Các điểm O,A,B có thẳng không?
b. Tìm M(x;y) để OABM là hình bình hành.
a: \(\overrightarrow{OA}=\left(2;1\right)\)
vecto OB=(3;3)
Vì 2/3<>1/3
nên O,A,B không thẳng hàng
b: Để OABM là hình bình hành thì vecto OA=vecto MB
\(\Leftrightarrow\left\{{}\begin{matrix}3-x_M=2\\3-y_M=1\end{matrix}\right.\Leftrightarrow M\left(1;2\right)\)
a: Để hai vecto cùng phương thì \(\dfrac{2m}{-4}=\dfrac{3m+1}{-8}\)
=>-16m=-4(3m+1)
=>3m+1=4m
=>-m=-1
=>m=1
b: vecto u=(a;b)
Theo đề, ta có: a^2+b^2=1 và a/-4=b/-8
=>a/1=b/2=k
=>a=k; b=2k
a^2+b^2=1
=>5k^2=1
=>k^2=1/5
TH1: k=1/căn 5
=>a=1/căn 5; b=2/căn 5
TH2: k=-1/căn 5
=>a=-1/căn 5; b=-2/căn 5
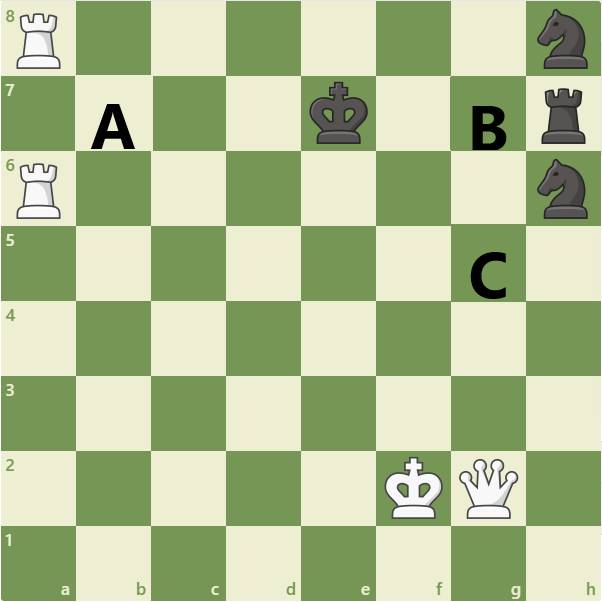
Trong hình bên, để bên Trắng chiếu hết thì trắng phải đi quân Hậu sang vị trí nào?
A. b7
B. g7
C. g5