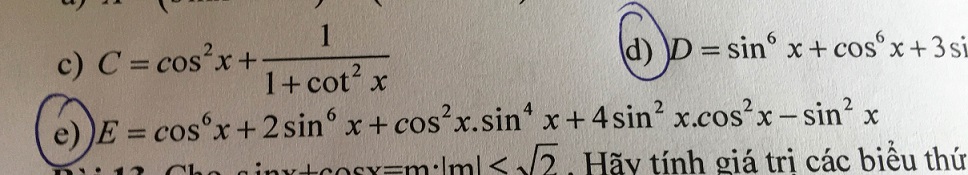Chứng minh rằng, với mọi tam giác ABC ta đều có: a) sinA = sin(B + C) b) cosA = -cos(B + C)
§1. Giá trị lượng giác của một góc bất kỳ từ 0 (độ) đến 180 (độ)
a: Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(\widehat{A}=180^0-\widehat{B}-\widehat{C}\)
=>\(sinA=sin\left(180-B-C\right)\)
=>\(sinA=sin\left(B+C\right)\)
b: Ta có: \(\widehat{A}=180^0-\widehat{B}-\widehat{C}\)
=>\(cosA=cos\left(180-\left(B+C\right)\right)\)
=>\(cosA=-cos\left(B+C\right)\)
Đúng 0
Bình luận (0)
cho tam giác ABC. Tìm tập hợp điểm M thỏa mãn |MA +MB+ MC|=1
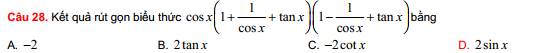
chỉ mih câu này vs cảm ơn
cosx(1 + 1/cosx + tanx)(1 - 1/cosx + tanx)
= cosx[(1 + tanx)² - 1/cos²x]
= cosx(1 + tan²x + 2tanx - 1 - tan²x)
= 2tanxcosx
= 2sinxcosx/cosx
= 2sinx
Chọn D
Đúng 0
Bình luận (0)
\(=cosx\left(1+\dfrac{1}{cosx}+\dfrac{sinx}{cosx}\right)\left(1-\dfrac{1}{cosx}+\dfrac{sinx}{cosx}\right)\)
\(=cosx\left(\dfrac{sinx+1+cosx}{cosx}\right)\left(\dfrac{cosx+sinx-1}{cosx}\right)\)
\(=\left(cosx+sinx\right)^2\)\(-1\)
\(=cos^2x+2cosxsinx+sin^2x-1\)
\(=cos^2x+sin^2x+2cosxsinx-1\)
\(=1+2cosxsinx-1\)
\(=2cosxsinx\)
Áp dụng đẳng thức góc nhân đôi cho sin
\(=2sinx\)
Đúng 0
Bình luận (0)
Chứng minh các biểu thức khồn phụ thuộc vào x
Đúng 0
Bình luận (0)
\(E=\left(cos^6x+sin^6x\right)+sin^4x\left(sin^2x+cos^2x\right)+4sin^2x.cos^2x-sin^2x\)
\(=\left(cos^2x+sin^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)+sin^4x+4sin^2x.cos^2x-sin^2x\)
\(=1+sin^2x.cos^2x+sin^4x-sin^2x\)
\(=cos^2x+sin^2x\left(sin^2x+cos^2x\right)\)
\(=cos^2x+sin^2x=1\)
Đúng 0
Bình luận (0)
Giúp mk bài 3 với ạ. Gấp ạ 
Cos0+cos20+cos40+...+cos160+cos180
\(=cos0^0+cos20^0+cos40^0+...+cos\left(180^0-40^0\right)+cos\left(180^0-20^0\right)+cos\left(180^0-0^0\right)\)
\(=cos0^0+cos20^0+cos40^0+...+\left(-cos40^0\right)+\left(-cos20^0\right)+\left(-cos0^0\right)\)
\(=0\)
Đúng 1
Bình luận (0)
Sin^2 45-2sin^2 50+3cos^2 45-2sin^2 40+4tan55.tan35 Giúp mình với ạ
\(=\left(\dfrac{\sqrt{2}}{2}\right)^2-2sin^2\left(90^0-40^0\right)+3\left(\dfrac{\sqrt{2}}{2}\right)^2-2sin^240^0+4tan55^0.tan\left(90^0-55^0\right)\)
\(=\dfrac{1}{2}+\dfrac{3}{2}-2cos^240^0-2sin^240^0+4tan55^0.cot55^0\)
\(=2-2\left(sin^240^0+cos^240^0\right)+4\)
\(=2-2+4=4\)
Đúng 0
Bình luận (0)
tính giá trị biểu thức A=\(cot20^o+cot40^o+...+cot140^o+cot160^o\)
A=cot20+cot160+cot40+cot140+...+cot80+cot100
=0+0+0+0
=0
Đúng 0
Bình luận (0)
\(\text{A=cot20+cot160+cot40+cot140+...+cot80+cot100}\)
\(=0+0+0+0\)
\(=0\)
Đúng 0
Bình luận (0)
cho sina+cosa=1 tính \(sin^3a+cos^3a\)
\(sinacosa=\dfrac{\left(sina+cosa\right)^2-1}{2}=\dfrac{1-1}{2}=0\)
\(sin^3a+cos^3a=\left(sina+cosa\right)^3-3cosa\cdot sina\left(sina+cosa\right)=1\)
Đúng 3
Bình luận (0)
\(sinacosa=\dfrac{\left(sina+cosa\right)^2-1}{2}=\dfrac{1-1}{2}=0\)
\(sin^3a+cos^3a=\left(sina+cosa\right)^3-3cosa.sina\)\(\left(sina+sosa\right)=1\)
Đúng 2
Bình luận (0)
cho tan a=3,tính giá trị biểu thức A=\(\dfrac{2sina-cosa}{sin^3a+2cos^3a}\)
`@1+tan^2 a=1/[cos^2 a]=>1+3^2=1/[cos^2 a]=>cos^2 a=1/10`
`@tan a=3=>[sin a]/[cos a]=3=>sin a=3cos a`
Thay vào `A` có: `A=[2.3cos a-cos a]/[(3cos a)^3+2cos^3 a]`
`A=[5cos a]/[29cos^3 a]=5/[29 cos^2 a]=5/[29. 1/10]=50/29`
Đúng 2
Bình luận (0)
tan a=3 nên sin a/cosa=3
=>sin a=3 cosa
\(A=\dfrac{2\cdot3cosa-cosa}{27\cdot cos^3a+2cos^3a}=\dfrac{5cosa}{29cos^3a}=\dfrac{5}{29cos^2a}\)
Đúng 1
Bình luận (0)