So sánh các góc của tam giác ABC, biết rằng :
AB = 2cm, BC = 4cm, AC = 5cm
So sánh các cạnh của tam giác ABC biết :
\(\widehat{A}=80^0;\widehat{B}=45^0\)
Tam giác ABC có = 800; = 450
Nên = 1800 – (800 + 450) = 550
(theo định lý tổng ba góc trong tam giác)
Vì 450 < 550 < 800 hay < < => AC < AB < BC
Trả lời bởi Tuyết Nhi MelodyCho tam giác ABC với \(\widehat{A}=100^0;\widehat{B}=40^0\)
a) Tìm cạnh lớn nhất của tam giác ABC ?
b) Tam giác ABC là tam giác gì ?
a) Tam giác ABC có = 1000 , = 400
Cạnh lớn nhất của tam giác ABC là BC vì BC đối diện với góc A và góc = 1000 > 900 nên góc A là góc tù
b) Tam giác ABC là tam giác tù
Trả lời bởi Tuyết Nhi MelodyTrong một tam giác, đối diện với cạnh nhỏ nhất là góc gì (nhọn, vuông, tù) ? Tại sao ?
Trong một tam giác, đối diện với cạnh nhỏ nhất là góc nhọn vì nếu góc đó là góc vuông hoặc tù thì hai góc còn lại phải lớn hơn góc vuông nên tổng ba góc của tam giác lớn hơn 1800 ( vô lý với định lý tổng ba góc của tam giác)
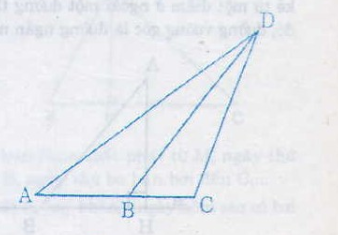
Trả lời bởi Tuyết Nhi MelodyBa bạn Hạnh, Nguyên, Trang đi đến trường theo ba con đường AD, BD và CD (h.5). Biết rằng ba điểm A, B, C cùng nằm trên một đường thẳng và góc ACD là góc tù.
Hỏi ai đi xa nhất, ai đi gần nhất ? Giải thích ?
Vì . = 900 nên ∆DCB có
=> BD > CD (1)
∆ABD có là góc ngoài của ∆DCB
=> >
nên là góc lớn nhất (vì tù)
=> AD > BD (2)
Từ (1) và (2) => AD > BD >CD
Vậy Hạnh đi xa nhất, Trang đi gần nhất
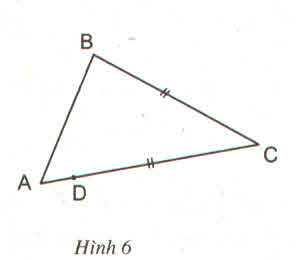
Xem hình 6, có hai đoạn thẳng bằng nhau BC và DC. Hỏi rằng kết luận nào trong các kết luận sau là đúng ? Tại sao ?
a) \(\widehat{A}=\widehat{B}\)
b) \(\widehat{A}>\widehat{B}\)
c) \(\widehat{A}< \widehat{B}\)
Một cách chứng minh khác của định lí 1 :
Cho tam giác ABC với AC >AB. Trên tia AC, lấy điểm B' sao cho AB' = BA
a) Hãy so sánh góc ABC với góc ABB'
b) Hãy so sánh góc ABB' với góc AB'B
c) Hãy so sánh góc AB'B với góc ACB
Từ đó suy ra \(\widehat{ABC}=\widehat{ACB}\)
a) Trên tia AC, AB' = AB
mà AB < AC ( giả thiết)
nên B' nằm giữa hai tia BA và BC
=> tia BB' nằm giữa hai tia BA và BC
=>
b) ∆ABB' có AB = AB' nên cân tại A
=>
c) Vì là góc ngoài tại B' của ∆BB'C nên
Vì (câu a)
(câu b)
(câu c)
=>
Trả lời bởi Tuyết Nhi MelodySo sánh các góc của tam giác ABC biết rằng \(AB=5cm,BC=5cm,AC=3cm\) ?
từ đề bài, ta có:
AB = BC >AC
\(\Rightarrow\widehat{C}=\widehat{A}>\widehat{B}\)
Trả lời bởi Hoàng Thu HồngSo sánh các cạnh của tam giác ABC biết \(\widehat{A}=80^0,\widehat{C}=40^0\) ?
Giải:
Ta có: \(\widehat{A}=80^0\)
\(\widehat{C}=40^0\)
\(\Leftrightarrow\widehat{B}=180^0-80^0-40^0=60^0\) (Tổng ba góc của một tam giác)
Suy ra: \(\widehat{A}>\widehat{B}>\widehat{C}\)
\(\Leftrightarrow BC>AC>AB\) (Tính chất giữa góc và cạnh đối diện)
Vậy ...
Trả lời bởi GiangCho tam giác ABC có \(\widehat{B}>90^0\), điểm D nằm giữa B và C.
Chứng minh rằng : AB < AD < AC
Xét ΔABD có \(\widehat{B}>90^0\)
nen AD là cạnh lớn nhất
=>AB<AD(1)
XétΔADC có \(\widehat{ADC}>90^0\)
nên AC là cạnh lớn nhất
=>AD<AC(2)
Từ (1) và (2) suy ra AB<AD<AC
Trả lời bởi Nguyễn Lê Phước Thịnh
Trong tam giác ABC có:
AB = 2cm ; BC = 4cm ; AC = 5cm
=> AB < BC < CA nên ˆC<ˆA<ˆB
Trả lời bởi Tuyết Nhi Melody