Kết luận đúng là c vì AC > BC nên
Đúng 0
Bình luận (0)
Bài 1: Quan hệ giữa góc và cạnh đối diện trong một tam giác
Các câu hỏi tương tự
Tam giác ABC có AB 5cm, BC 6cm và AC 7 cm. Gọi widehat{A}_1,widehat{B}_1,widehat{C}_1 theo thứ tự là góc ngoài tại đỉnh A, B, C của tam giác đó. Trong các khẳng định sau, khẳng định nào đúng ?
(A) widehat{A}_1widehat{B}_1widehat{C}_1 (B) widehat{B}_1widehat{C}_1widehat{A}_1
(C) widehat{C}_1widehat{A}_1widehat{B}_1 (D) widehat{C}_1widehat{B}_1widehat{A}_1
Đọc tiếp
Tam giác ABC có AB = 5cm, BC = 6cm và AC = 7 cm. Gọi \(\widehat{A}_1,\widehat{B}_1,\widehat{C}_1\) theo thứ tự là góc ngoài tại đỉnh A, B, C của tam giác đó. Trong các khẳng định sau, khẳng định nào đúng ?
(A) \(\widehat{A}_1>\widehat{B}_1>\widehat{C}_1\) (B) \(\widehat{B}_1>\widehat{C}_1>\widehat{A}_1\)
(C) \(\widehat{C}_1>\widehat{A}_1>\widehat{B}_1\) (D) \(\widehat{C}_1>\widehat{B}_1>\widehat{A}_1\)
H24
3 tháng 3 2020 lúc 21:38
1. Cho △ABC có AB là cạnh lớn nhất, BC là cạnh nhỏ nhất. Chứng minh rằng widehat{C}60^o, widehat{A}le60^o.
2. Cho tam giác ABC có M là trung điểm BC.
a) Giả sử AB AC. Chứng minh widehat{MAC} widehat{BAM}
b) Giả sử widehat{MAC} widehat{BAM}. Chứng minh AB AC.
c) Gọi N là trung điểm AC, AM cắt BN tại G. Giả sử AM ⊥ BN. Chứng minh 2AC BC.
3.
a) Cho △ABC cân tại A, D là điểm bất kì trong △ABC sao cho widehat{ADB} widehat{ADC}. Chứng minh BD DC
b) Cho △ABC vuông tại A. Chứng minh rằng AB^...
Đọc tiếp
1. Cho △ABC có AB là cạnh lớn nhất, BC là cạnh nhỏ nhất. Chứng minh rằng \(\widehat{C}>60^o\), \(\widehat{A}\le60^o\).
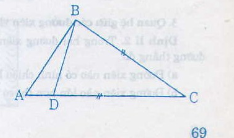
2. Cho tam giác ABC có M là trung điểm BC.
a) Giả sử AB < AC. Chứng minh \(\widehat{MAC}< \widehat{BAM}\)
b) Giả sử \(\widehat{MAC}< \widehat{BAM}\). Chứng minh AB < AC.
c) Gọi N là trung điểm AC, AM cắt BN tại G. Giả sử AM ⊥ BN. Chứng minh 2AC > BC.
3.
a) Cho △ABC cân tại A, D là điểm bất kì trong △ABC sao cho \(\widehat{ADB}< \widehat{ADC}\). Chứng minh BD > DC
b) Cho △ABC vuông tại A. Chứng minh rằng \(AB^{2017}+AC^{2017}< BC^{2017}\)
Tam giác ABC có \(\widehat{A}\) là góc tù, \(\widehat{B}>\widehat{C}\). Trong các khẳng định sau, khẳng định nào đúng ?
(A) AB > AC > BC (B) AC > AB > BC
(C) BC > AB > AC (D) BC > AC > AB
Cho \(\Delta ABC\) có \(\widehat{A}=50^0;\widehat{B}:\widehat{C}=2:3\). So sánh các cạnh của \(\Delta ABC\)
Cho tam giác ABC vuông ở A. M là trung điểm của AC. Trên tia đối của tia MB lấy điểm D sao cho MD = MB. Chứng minh rằng:
a) CD \(\perp\) AC và BC > CD
b) \(\widehat{ABM}>\widehat{MBC}\)
Cho tam giác ABC với \(\widehat{A}=100^0;\widehat{B}=40^0\)
a) Tìm cạnh lớn nhất của tam giác ABC ?
b) Tam giác ABC là tam giác gì ?
Chứng minh định lí "Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn" theo gợi ý sau :
Cho tam giác ABC có \(\widehat{B}>\widehat{C}\)
a) Có thể xảy ra AC < AB hay không ?
b) Có thể xảy ra AC = AB hay không ?
So sánh các cạnh của tam giác ABC biết :
\(\widehat{A}=80^0;\widehat{B}=45^0\)
Cho tam giác vuông ABC, \(\widehat{A}\) = 90độ. Chứng minh rằng \(\widehat{C}\) = 30độ khi và chỉ khi AB=\(\dfrac{1}{2}\)BC.