Vẽ một tam giác vuông có một góc nhọn \(34^0\) rồi viết các tỉ số lượng giác của góc \(34^0\) ?
Cho tam giác ABC vuông tại C, trong đó AC =0,9m, BC = 1,2m. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc A ?
sinA=cosB=0,8sinA=cosB=0,8
cosA=sinB=0,6cosA=sinB=0,6
tgA=cotgB=43≈1,33tgA=cotgB=43≈1,33
cotgA=tgB=0,75cotgA=tgB=0,75.
Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn \(45^0\):
\(\sin60^0;\cos75^0;\sin52^030';cotg82^0;tg80^0\)
Vận dụng định lý về tỉ số lượng giác của hai góc phụ nhau ta có:
sin60° = cos(90° – 60°) = cos30°
Tương tự:
cos75° = sin(90° – 75°) = sin 15°
sin52°30′ = cos(90° – 52°30′) = 38°30′
cotg82° = tg8°; tg80° = cotg10°
Trả lời bởi Nhật LinhDựng góc nhọn \(\alpha\), biết :
a) \(\sin\alpha=\dfrac{2}{3}\)
b) \(\cos\alpha=0,6\)
c) \(tg\alpha=\dfrac{3}{4}\)
d) \(cotg\alpha=\dfrac{3}{2}\)
Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh rằng : Với góc nhọn \(\alpha\) tùy ý, ta có :
a) \(tg\alpha=\dfrac{\sin\alpha}{\cos\alpha}\)
\(cotg\alpha=\dfrac{\cos\alpha}{\sin\alpha}\)
\(tg\alpha.cotg\alpha=1\)
b) \(\sin^2\alpha+\cos^2\alpha=1\)
Gợi ý : Sử dụng định lí Pytago
Hướng dẫn giải:
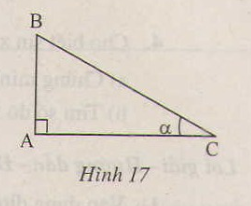
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khá
Trả lời bởi Thien Tu Borum
Cho tam giác ABC vuông tại A. Biết \(\cos B=0,8\), hãy tính các tỉ số lượng giác của góc C
Gợi ý : Sử dụng bài tập 14
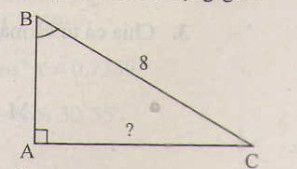
Cho tam giác vuông có một góc \(60^0\) và cạnh huyền có độ dài là 8. Hãy tìm độ dài của cạnh đối diện với góc \(60^0\)
Tìm x trong hình 23 ?
Vẽ một tam giác vuông có một góc nhọn bằng \(40^0\) rồi viết các tỉ số lượng giác của góc \(40^0\) ?
Cho tam giác ABC vuông tại A. Chứng minh rằng :
\(\dfrac{AC}{AB}=\dfrac{\sin B}{\sin C}\)
\(\dfrac{\sin B}{\sin C}=\dfrac{AC}{BC}:\dfrac{AB}{BC}=\dfrac{AC}{AB}\)
Trả lời bởi Nguyễn Lê Phước Thịnh
Vẽ tam giác ABC vuông tại A, góc C = 34°
Theo định nghĩa ta có:
Trả lời bởi Nhật Linh