Question

Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì  ? Vì sao ?

Answer 1

Xét \(\Delta ABC\) có:

E là trung điểm AB (gt)

F là trung điểm AC (gt)

=> EF là đường trung bình \(\Delta ABC\) (ĐN đường TB \(\Delta\))

=> EF // AC, \(EF=\dfrac{AC}{2}\) (tính chất đường TB \(\Delta\))

Xét \(\Delta ADC\) có:

H là trung điểm AD

G là trung điểm DC

=> HG là đường trung bình \(\Delta ADC\) (ĐN đường TB \(\Delta\))

=> HG // AC, \(HG=\dfrac{BC}{2}\) (tính chất đường TB \(\Delta\))

Ta có: EF // AC, HG // AC

\(EF=\dfrac{AC}{2},HG=\dfrac{AC}{2}\)

=> EF // HG, EF = HG

Xét tứ giác EFGH có:

EF // HG

EF = HG

=> EFGH là hình bình hành (dhnb)

Answer 2

Tứ giác EFGH là hình bình hành.

Cách 1: EB = EA, FB = FC (gt)

nên EF là đường trung bình của ∆ABC.

Do đó EF // AC

Tương tự HG là đường trung bình của ∆ACD.

Do đó HG // AC

Suy ra EF // HG (1)

Tương tự EH // FG (2)

Từ (1) và (2) suy ra EFGH là hình bình hành (dấu hiêu nhận biết 1).

Cách 2: EF là đường trung bình của ∆ABC nên EF = AC.

HG là đường trung bình của ∆ACD nên HG = AC.

Suy ra EF = HG

Lại có EF // HG ( chứng minh trên)

Vậy EFGH là hình bình hành (dấu hiệu nhận biết 3).

Answer 3

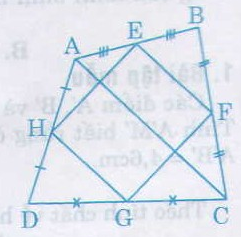
TỨ giác ABCD có E,F,G,Htheo thứ tự là trung diểm của các cạnh AB,BC,CD,DA.Chứng minh EF//GH,EH//FG