Trên một đường tròn, lấy liên tiếp ba cung AC, CD, DB sao cho số đo cung AC bằng số đo cung CD bằng số đo cung DB và bằng 60o. Hai đường thẳng AC và BD cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:
a) \(\widehat{AEB}=\widehat{BTC}.\)
b) CD là tia phân giác của \(\widehat{BCT}.\)
a) Ta có 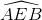 là góc có đỉnh ở bên ngoài đường tròn nên:
là góc có đỉnh ở bên ngoài đường tròn nên:
\(\widehat{AEB}=\dfrac{sđ\left(\widehat{AB}-\widehat{CD}\right)}{2}=\dfrac{180^O-60^O}{2}=60^O\)
và \(\widehat{BTC}\) cũng là góc có đỉnh ở bên ngoài đường tròn ( hai cạnh đều là tiếp tuyến của đường tròn) nên:
\(\widehat{BTC}\) = sđ\(\dfrac{\widehat{BAC}-\widehat{BDC}}{2}=\dfrac{\left(180^O+60^O\right)-\left(60^O+60^O\right)}{2}=60^O\)
Vậy 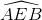 =
=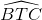
b) \(\widehat{DCT}\) là góc tạo bởi tiếp tuyến và dây cung nên:
\(\widehat{DCT}=\dfrac{sđ\widehat{CD}}{2}=\dfrac{60^o}{2}=30^o\)
→ \(\widehat{DCB}\) là góc nội tiếp trên
\(\widehat{DCB}\) = \(\dfrac{sđ\widehat{DB}}{2}\) = \(\dfrac{60^O}{2}=30^O\)
Vậy \(\widehat{DCT}\) = \(\widehat{DCB}\) hay CD là phân giác của \(\widehat{BCT}\)


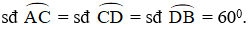 Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:
Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:
