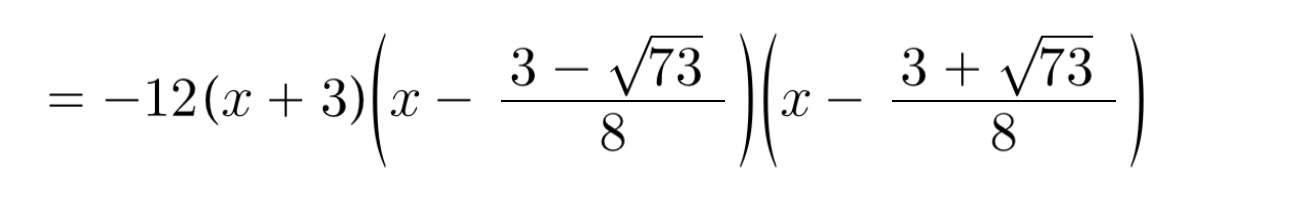\(a,x^2-y^2-2yz-z^2\\ =x^2-\left(y^2+2yz+z^2\right)\\ =x^2-\left(y+z\right)^2\\ =\left(x-y-z\right)\left(x+y+z\right)\\ b,3a^2-6ab+3b^2-12c^2\\ =3\left(a^2-2ab+b^2-4c^2\right)\\ =3\left[\left(a-b\right)^2-\left(2c\right)^2\right]\\ =3\left(a-b-2c\right)\left(a-b+2c\right)\\ c,x^2-2xy+y^2-m^2+2mn-n^2\\ =\left(x^2-2xy+y^2\right)-\left(m^2-2mn+n^2\right)\\ =\left(x-y\right)^2-\left(m-n\right)^2\\ =\left(x-y-m+n\right)\left(x-y+m-n\right)\\ d,a^2-10a+25-y^2-4yz-4z^2\\ =\left(a^2-10a+25\right)-\left(y^2+4yz+4z^2\right)\\ =\left(a-5\right)^2-\left(y+2z\right)^2\\ =\left(a-5-y-2z\right)\left(a-5+y+2z\right)\)
a) x² - y² - 2yz - z²
= x² - (y² + 2yz + z²)
= x² - (y + z)²
= (x - y - z)(x + y + z)
b) 3a² - 6ab + 3b² - 12c²
= 3(a² - 2ab + b² - 4c²)
= 3[(a² - 2ab + b²) - (2c)²]
= 3[(a - b)² - (2c)²]
= 3(a - b - 2c)(a - b + 2c)
c) x² - 2xy + y² - m² + 2mn - n²
= (x² - 2xy + y²) - (m² - 2mn + n²)
= (x - y)² - (m - n)²
= (x - y - m + n)(x - y + m - n)
d) a² - 10a + 25 - y² - 4yz - 4z²
= (a² - 10a + 25) - (y² + 4yz + 4z²)
= (a - 5)² - (y + 2z)²
= (a - 5 - y - 2z)(a - 5 + y + 2z)
e) x² + 3cd(2 - 3cd) - 10xy - 1 + 25y²
= (x² - 10xy + 25y²) + 6cd - 9c²d² - 1
= (x - 5)² - (9c²d² - 6cd + 1)
= (x - 5)² - (3cd - 1)²
= (x - 5 - 3cd + 1)(x - 5 + 3cd - 1)
f) 4b²c² - (b² + c² - a²)²
= (2bc)² - (b² + c² - a²)²
= (2bc - b² - c² + a²)(2bc + b² + c² - a²)
= [a² - (b² - 2bc + c²)][(b² + 2bc + c²) - a²]
= [a² - (b - c)²][(b + c)² - a²]
= (a - b + c)(a + b - c)(b + c - a)(b + c + a)
g) (4x² - 3x - 18)² - (4x² + 3x)²
= (4x² - 3x - 18 - 4x² - 3x)(4x² - 3x - 18 + 4x² - 3x)
= (-6x - 18)(8x² - 6x - 18)
= -6.2(x + 3)(4x² - 3x - 4)