1) Thay x= 9 vào Q ta được :
√9 + 1 / √ 9 - 2 = 3 + 1 / 3 - 2 = 4
1) Thay x= 9 vào Q ta được :
√9 + 1 / √ 9 - 2 = 3 + 1 / 3 - 2 = 4
1) thay x = 9 vào Q ta được
\(\dfrac{\sqrt{9}+1}{\sqrt{9}-2}=\dfrac{3+1}{3-2}=\dfrac{4}{1}=4\)
2) ta có: \(P=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{\sqrt{x}}{\sqrt{x}+2}-\dfrac{3\sqrt{x}-2}{4-x}\)
\(P=\dfrac{\left(\sqrt{x}+1\right)\cdot\left(\sqrt{x}+2\right)+\sqrt{x}\cdot\left(\sqrt{x}-2\right)+3\sqrt{x}-2}{\left(\sqrt{x}+2\right)\cdot\left(\sqrt{x}-2\right)}\\ P=\dfrac{x+2\sqrt{x}+\sqrt{x}+2+x-2\sqrt{x}+3\sqrt{x}-2}{\left(\sqrt{x}+2\right)\cdot\left(\sqrt{x}-2\right)}\\ P=\dfrac{2x+4\sqrt{x}}{\left(\sqrt{x}+2\right)\cdot\left(\sqrt{x}-2\right)}\\ P=\dfrac{2\sqrt{x}\cdot\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\cdot\left(\sqrt{x}-2\right)}\\ P=\dfrac{2\sqrt{x}\cdot\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\cdot\left(\sqrt{x}-2\right)}\\ P=\dfrac{2\sqrt{x}}{\left(\sqrt{x}-2\right)}\)
3) \(M=P:Q=\dfrac{2\sqrt{x}}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}+1}=\dfrac{2\sqrt{x}}{\sqrt{x}+1}\\ =\dfrac{\sqrt{x}+1+\sqrt{x}-1}{\sqrt{x}+1}=1+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
để M đạt giá trị nguyên thì [√(x) - 1] / [√(x) + 1] đạt giá trị nguyên
\(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{\sqrt{x}+1-2}{\sqrt{x}+1}=1-\dfrac{2}{\sqrt{x}+1}\)
=> √(x) + 1 ∈ Ư(2) = {±1; ±2}
\(\sqrt{x}+1=1\Rightarrow x=0\left(TM\right)\\ \sqrt{x}+1=-1\Rightarrow\left(\text{vô nghiệm}\right)\\ \sqrt{x}+1=2\Rightarrow x=1\left(KTM\right)\\ \sqrt{x}+1=-2\Rightarrow\text{vô nghiệm}\)
vậy để M nhận giá trị nguyên thì x = 0
Câu II:
1: Thay x=9 vào Q, ta được:
\(Q=\dfrac{3+1}{3-2}=\dfrac{4}{1}=4\)
2: \(P=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{\sqrt{x}}{\sqrt{x}+2}-\dfrac{3\sqrt{x}-2}{4-x}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{\sqrt{x}}{\sqrt{x}+2}+\dfrac{3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)+\sqrt{x}\left(\sqrt{x}-2\right)+3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+3\sqrt{x}+2+x-2\sqrt{x}+3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{2x+4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}-2}\)
3: \(M=P:Q=\dfrac{2\sqrt{x}}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}-2}=\dfrac{2\sqrt{x}}{\sqrt{x}+1}\)
Để M là số nguyên thì \(2\sqrt{x}⋮\sqrt{x}+1\)
=>\(2\sqrt{x}+2-2⋮\sqrt{x}+1\)
=>\(-2⋮\sqrt{x}+1\)
=>\(\sqrt{x}+1\in\left\{1;2\right\}\)
=>\(\sqrt{x}\in\left\{0;1\right\}\)
=>\(x\in\left\{0;1\right\}\)

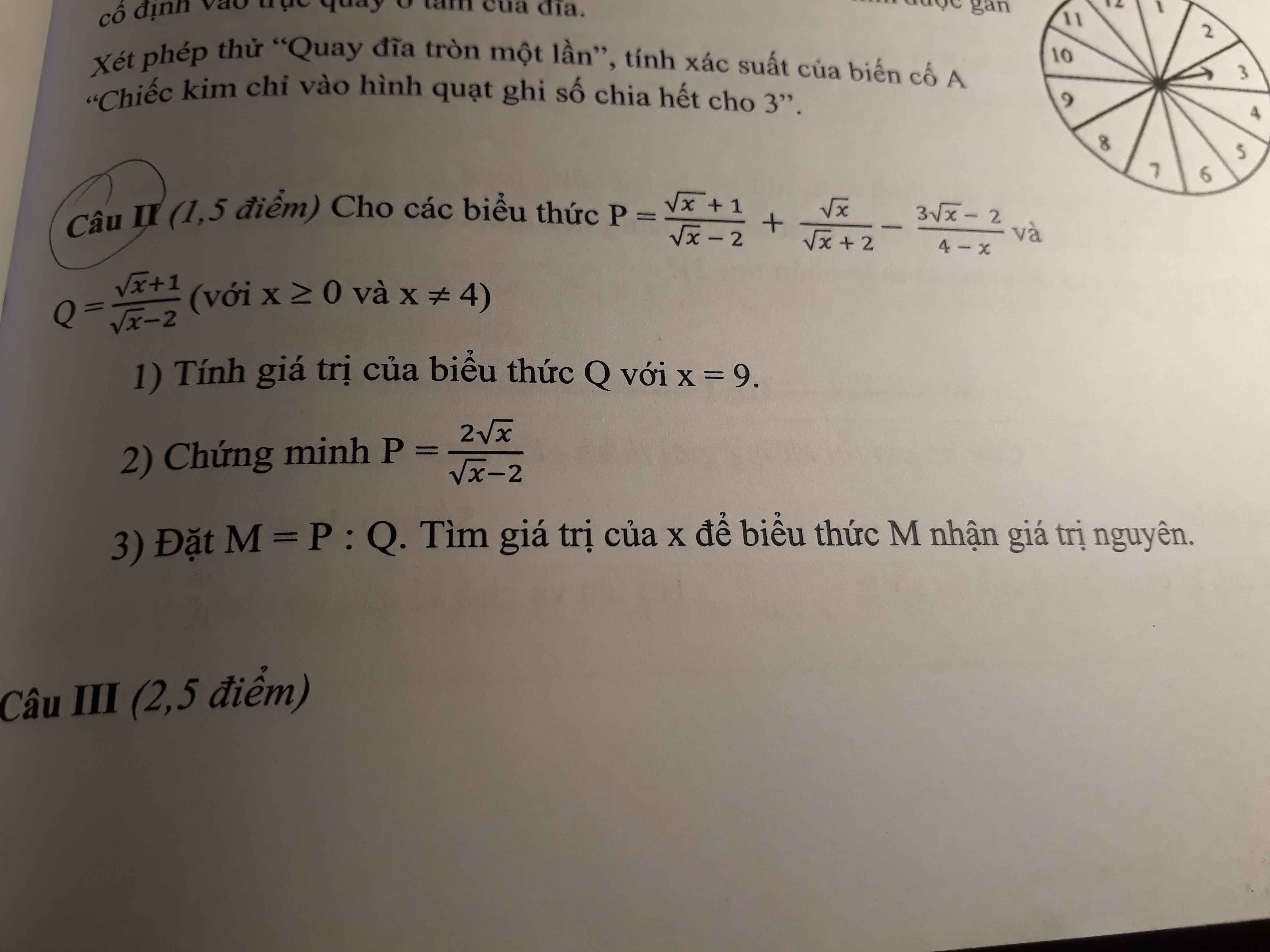





 không cần làm câu c đâu ạ, giúp e với nhaaa mn
không cần làm câu c đâu ạ, giúp e với nhaaa mn