a: Ta có: \(A=\sqrt{6+2\sqrt{5-\sqrt{13+\sqrt{48}}}}\)
\(=\sqrt{6+2\sqrt{4-2\sqrt{3}}}\)
\(=\sqrt{6+2\cdot\left(\sqrt{3}-1\right)}\)
\(=\sqrt{3}-1\)
Ta có: \(\dfrac{1}{\sqrt{7-\sqrt{24}}-1}-\dfrac{1}{\sqrt{7+\sqrt{24}}-1}\)
\(=\dfrac{1}{\sqrt{6}-1-1}-\dfrac{1}{\sqrt{6}+1-1}\)
\(=\dfrac{1}{\sqrt{6}-2}-\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{\sqrt{6}+2}{2}-\dfrac{\sqrt{6}}{6}\)
\(=\dfrac{3\sqrt{6}+6-\sqrt{6}}{6}\)
\(=\dfrac{2\sqrt{6}+6}{6}\)
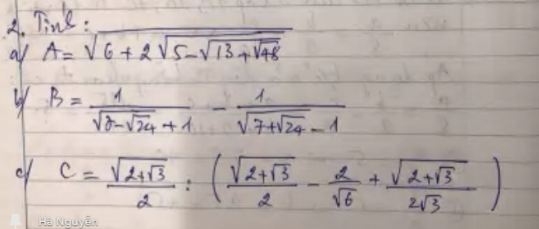


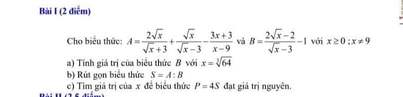

 giúp mk với
giúp mk với
