d: ĐKXĐ: x>=0
\(\dfrac{\sqrt{x}-1}{\sqrt{x}+3}=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}\)
=>\(\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)=\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)\)
=>\(x-2\sqrt{x}+3\sqrt{x}-6=x-1\)
=>\(\sqrt{x}-6=-1\)
=>\(\sqrt{x}=5\)
=>x=25(nhận)
e: ĐKXĐ: x>1
\(\dfrac{\sqrt{x^2+2x-3}}{\sqrt{x-1}}=x+3\)
=>\(\sqrt{\dfrac{x^2+2x-3}{x-1}}=x+3\)
=>\(\sqrt{x+3}=x+3\)
=>\(\sqrt{x+3}\left(\sqrt{x+3}-1\right)=0\)
=>\(\left[{}\begin{matrix}\sqrt{x+3}=0\\x+3=1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-3\left(loại\right)\\x=-2\left(loại\right)\end{matrix}\right.\)
f: ĐKXĐ: x>0
\(\sqrt{x}+\sqrt{x+1}=\dfrac{1}{\sqrt{x}}\)
=>\(\dfrac{x+1-x}{\sqrt{x+1}-\sqrt{x}}=\dfrac{1}{\sqrt{x}}\)
=>\(\dfrac{1}{\sqrt{x+1}-\sqrt{x}}=\dfrac{1}{\sqrt{x}}\)
=>\(\sqrt{x+1}-\sqrt{x}=\sqrt{x}\)
=>\(\sqrt{x+1}=2\sqrt{x}=\sqrt{4x}\)
=>4x=x+1
=>3x=1
=>\(x=\dfrac{1}{3}\left(nhận\right)\)
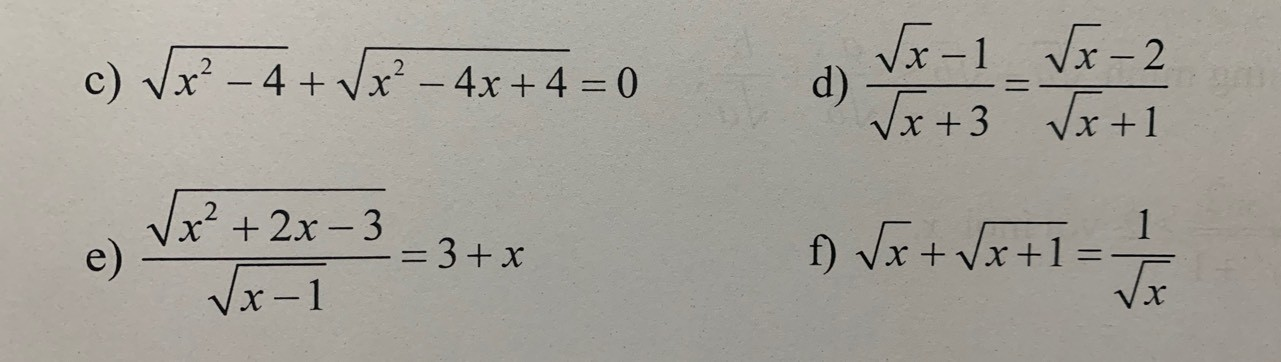





 Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.