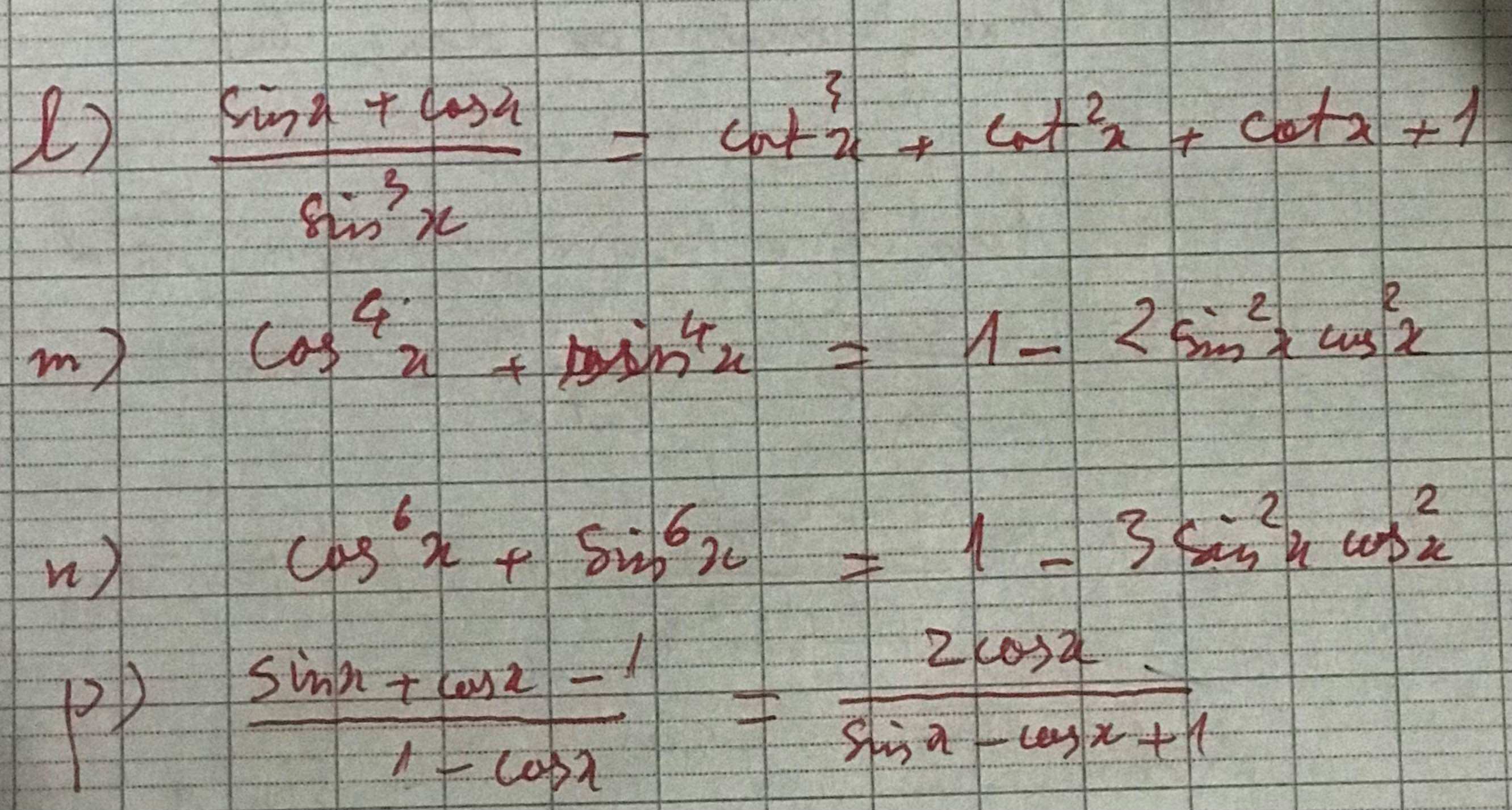m: \(sin^4x+cos^4x\)
\(=\left(sin^2x+cos^2x\right)^2-2\cdot sin^2x\cdot cos^2x\)
\(=1-2\cdot sin^2x\cdot cos^2x\)
n: \(cos^6x+sin^6x\)
\(=\left(sin^2x+cos^2x\right)^3-3\cdot sin^2x\cdot cos^2x\left(sin^2x+cos^2x\right)\)
\(=1-3\cdot sin^2x\cdot cos^2x\)
p: \(\left(sinx+cosx-1\right)\left(sinx-cosx+1\right)\)
\(=sin^2x-\left(cosx-1\right)^2\)
\(=sin^2x-\left(cos^2x-2\cdot cosx+1\right)\)
\(=sin^2x-cos^2x+2\cdot cosx-1\)
\(=sin^2x-cos^2x-sin^2x-cos^2x+2\cdot cosx\)
\(=2\cdot cosx-2\cdot cos^2x=2\cdot cosx\left(1-cosx\right)\)
=>\(\dfrac{sinx+cosx-1}{1-cosx}=\dfrac{2\cdot cosx}{sinx-cosx+1}\)
l: \(sin^3x\cdot\left(cot^3x+cot^2x+cotx+1\right)\)
\(=sin^3x\cdot\left(cot^2x+1\right)\left(cotx+1\right)\)
\(=\dfrac{sin^3x}{sin^2x}\cdot\left(cotx+1\right)=sinx\left(\dfrac{cosx}{sinx}+1\right)=cosx+sinx\)
=>\(\dfrac{sinx+cosx}{sin^3x}=cot^3x+cot^2x+cotx+1\)