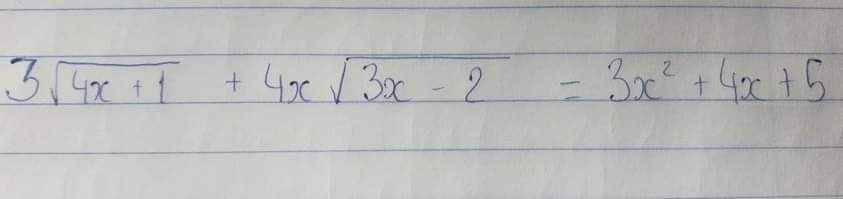\(3\sqrt{4x+1}+4x\sqrt{3x-2}=3x^{^2}+4x+5\Leftrightarrow12x+3+12x^2-8x=3x^2+4x+5\Leftrightarrow12x+12x^2-8x-3x^2-4x=5-3\Leftrightarrow9x^2=2\Leftrightarrow x^2=\dfrac{2}{9}\Leftrightarrow x=\dfrac{\sqrt{2}}{3}\)
ĐKXĐ: \(\left\{{}\begin{matrix}4x+1>=0\\3x-2>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-\dfrac{1}{4}\\x>=\dfrac{2}{3}\end{matrix}\right.\)
=>\(x>=\dfrac{2}{3}\)
\(3\sqrt{4x+1}+4x\sqrt{3x-2}=3x^2+4x+5\)
=>\(3\sqrt{4x+1}-9+4x\sqrt{3x-2}=3x^2+4x-4\)
=>\(3\left(\sqrt{4x+1}-3\right)+4x\sqrt{3x-2}=4x^2-8x-x^2+12x-4\)
=>\(3\cdot\dfrac{4x+1-9}{\sqrt{4x+1}+3}+4x\sqrt{3x-2}=3x^2+4x-4\)
=>\(3\cdot\dfrac{4x-8}{\sqrt{4x+1}+3}+4x\sqrt{3x-2}=3x^2-6x+10x-20+16\)
=>\(\dfrac{12\left(x-2\right)}{\sqrt{4x+1}+3}+4x\sqrt{3x-2}-16=\left(x-2\right)\left(3x+10\right)\)
=>\(\dfrac{12\left(x-2\right)}{\sqrt{4x+1}+3}+4\cdot\sqrt{3x^3-2x^2}-16=\left(x-2\right)\left(3x+10\right)\)
=>\(\dfrac{12\left(x-2\right)}{\sqrt{4x+1}+3}+4\cdot\dfrac{3x^3-2x^2-16}{\sqrt{3x^3+2x^2}+4}=\left(x-2\right)\left(3x+10\right)\)
=>\(\dfrac{12\left(x-2\right)}{\sqrt{4x+1}+3}+4\cdot\dfrac{3x^3-6x^2+4x^2-8x+8x-16}{\sqrt{3x^3+2x^2}+4}-\left(x-2\right)\left(3x+10\right)=0\)
=>\(\dfrac{12\left(x-2\right)}{\sqrt{4x+1}+3}+4\cdot\dfrac{\left(x-2\right)\left(3x^2+4x+8\right)}{\sqrt{3x^3+2x^2}+4}-\left(x-2\right)\left(3x+10\right)=0\)
=>\(\left(x-2\right)\left(\dfrac{12}{\sqrt{4x+1}+3}+\dfrac{4\left(3x^2+4x+8\right)}{\sqrt{3x^3+2x^2}+4}-3x-10\right)=0\)
=>x-2=0
=>x=2(nhận)
Anh thấy cách của anh Thịnh có vấn đề, nên anh làm cách của anh nhé:
\(ĐKXĐ:x\ge\dfrac{2}{3}\)
Ta sử dụng phương pháp bất đẳng thức (nghĩa là ta sẽ chứng minh làm sao cho \(VT\le VP\) hoặc ngược lại với điều kiện ban đầu):
Ta để ý nghiệm của phương trình ban đầu là \(x=2\), do đó ta phải áp dụng các bất đẳng thức quen thuộc sao cho điểm rơi xảy ra là 2.
Áp dụng bất đẳng thức Cauchy, ta có:
\(\sqrt{\left(4x+1\right).9}\le\dfrac{4x+1+9}{2}=2x+5\)
\(4x\sqrt{3x-2}\le4.\dfrac{x^2+\left(3x-2\right)}{2}=2\left(x^2+3x-2\right)\)
Cộng vế theo vế ta được:
\(3\sqrt{4x+1}+4x\sqrt{3x-2}\le2x^2+8x+1\)
Mặt khác \(2x^2+8x+1\le3x^2+4x+5\) (vì khi biến đổi tương đương bất đẳng thức trên, ta được \(\left(x-2\right)^2\ge0\), đây là một đánh giá hiển nhiên đúng).
Do đó: \(3\sqrt{4x+1}+4x\sqrt{3x-2}\le3x^2+4x+5\)
Đẳng thức xảy ra khi \(x=2\)
Kết hợp với phương trình ban đầu, ta được \(x=2\)
Vậy \(x=2\) là nghiệm của phương trình đã cho.