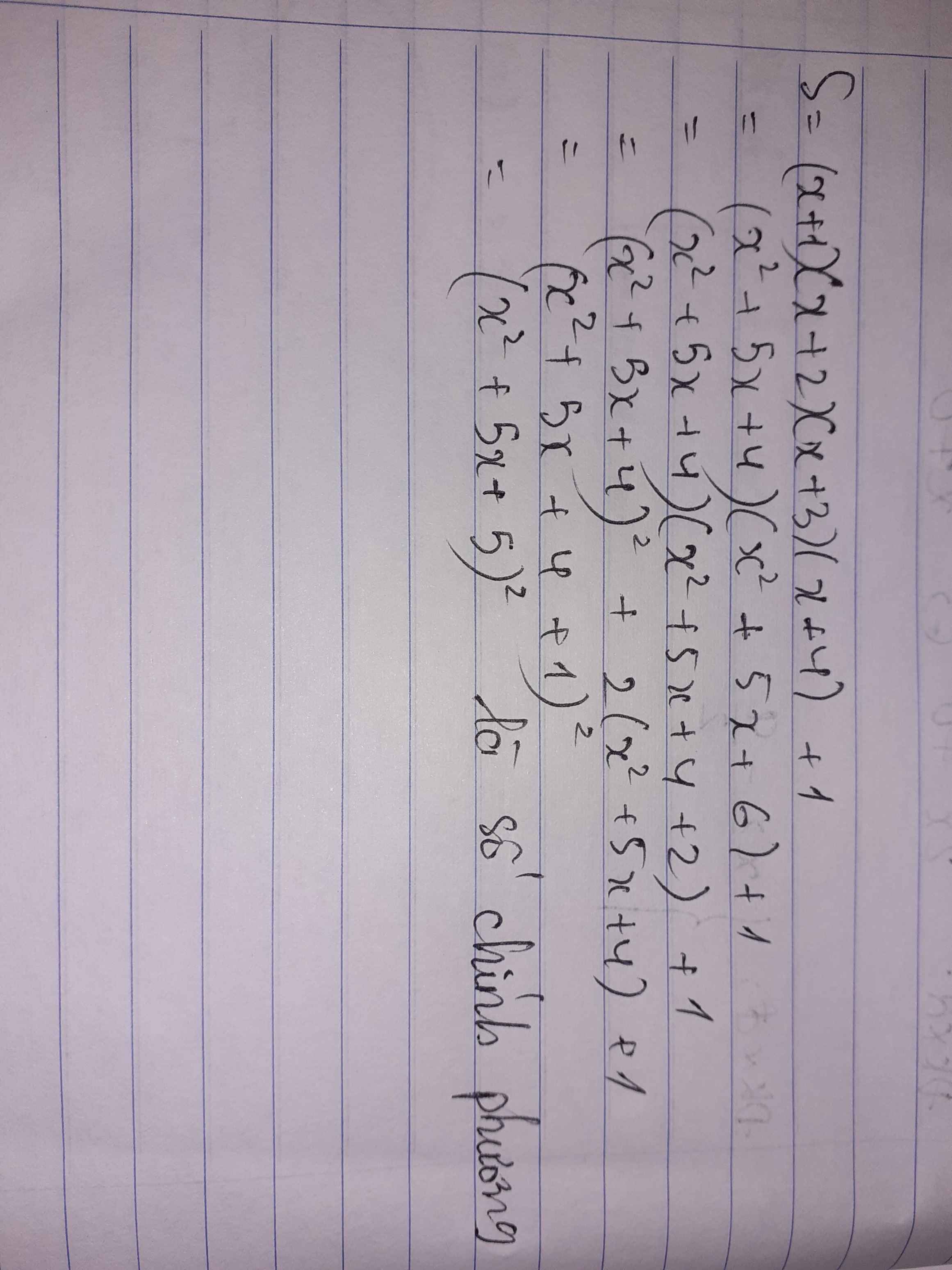\(S=\left(x+1\right)\left(x+4\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+4+2\right)+1\)
\(=\left(x^2+5x+4\right)^2+2\left(x^2+5x+4\right)+1\)
\(=\left(x^2+5x+4+1\right)^2\)
\(=\left(x^2+5x+5\right)^2\) là SCP (đpcm)
\(S=\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)+1=\left(x+1\right)\left(x+4\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1\)
Đặt \(t=x^2+5x+5\Rightarrow\) pt trở thành \(\left(t-1\right)\left(t+1\right)+1=t^2-1+1=t^2\)
\(=\left(x^2+5x+5\right)^2\)
Vì \(x\in Z\Rightarrow x^2+5x+5\in Z\Rightarrow\left(x^2+5x+5\right)^2\) là số chính phương
S = (x + 1)(x + 2)(x + 3)(x + 4) + 1
= [(x + 1)(x + 4)][(x + 2)(x + 3)] + 1
= (x^2 + 5x + 4)(x^2 + 5x +6) + 1
Đặt t = x^2 + 5x + 5 (do x ∈ Z nên t ∈ Z)
⇒ S = (t - 1)(t + 1) + 1
= t^2 - 1 + 1
= t^2 là số chính phương do t ∈ Z
⇒ S là số cp với mọi x ∈ Z (đpcm)
Ta có: \(S=\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1\)
\(=\left(x^2+5x\right)^2+10\left(x^2+5x\right)+24+1\)
\(=\left(x^2+5x\right)^2+10\left(x^2+5x\right)+25\)
\(=\left(x^2+5x+5\right)^2\)