Question

Chứng minh rằng trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.

Answer 1

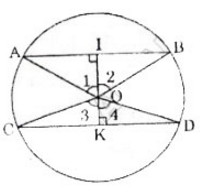
Giả sử AB và CD là các dây song song của đường tròn (O).

Kẻ OI ⊥ AB (I ∈ AB) và OK ⊥ CD (K∈CD).

Do AB //CD nên I,O,K thẳng hàng.

Do các tamgiác OAB, OCD là các tam giác cân đỉnh O nên các đường cao kẻ từ đỉnh đồng thời là phân giác.

Vì vậy ta có: Góc ∠O₁ = ∠O₂, ∠O₃ = ∠O₄

Giả sử AB nằm ngoài góc COD, ta có: ∠AOC = 1800 – (∠O₁ + ∠O₃) = 1800 -(∠O₂ + ∠O₄) = ∠BOD

Suy ra cung AC= cung BD.

Nghĩa là hai cung bị chắn giữa hai dây song song thì bằng nhau. Các trường hợp khác ta chứng minh tương tự.

Answer 2

Bài này có 2 TH, ta phải xét cả 2 TH (vì ko có ghi rõ đề):

TH 1:

Xét

AOB có:

OA = OB (cùng bán kính)

Do đó:

AOB cân tại A

Ta có:

(2 góc so le trong do AB//MN)

( // )

mà

(cmt)

(1)

CM tương tự, ta được:

(2)

Từ (1) và (2) suy ra \(\widehat{AOC}=\widehat{BOD}\)

\(\widebat{AC}=\widebat{BD}\)

TH 2 :

CM y như câu a) (mà chỉ thay đổi cách CM \(\widehat{AOC}=\widehat{BOD}\) )