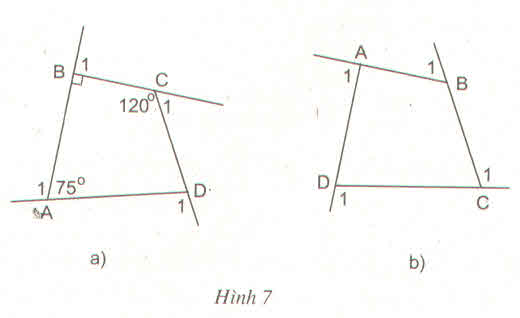
Gọi tứ giác là ABCD
Ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\\ \left(180^o-\widehat{A}\right)+\left(180^o-\widehat{B}\right)+\left(180^o-\widehat{C}\right)+\left(180^o-\widehat{D}\right)\\ =180^o-\widehat{A}+180^o-\widehat{B}+180^o-\widehat{C}+180^o-\widehat{D}\\ =\left(180^o+180^o+180^o+180^o\right)-\left(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}\right)\\ =180^o\cdot4-360^o\\ =720^o-360^o\\ =360^o\)
Vậy tổng các góc ngoài của tứ giác bằng tổng các góc trong của tứ giác