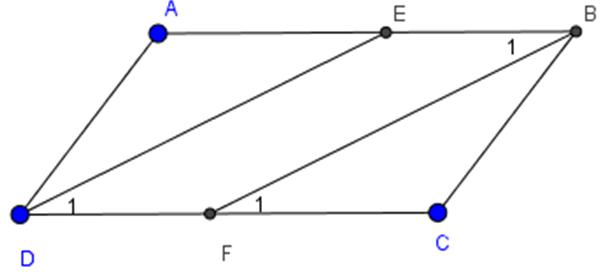
a) Ta có: \(\widehat{ADC}=\widehat{ABC}\)(ABCD là hình bình hành)
\(\Rightarrow\dfrac{1}{2}\widehat{ADC}=\dfrac{1}{2}\widehat{ABC}\Rightarrow\widehat{D_2}=\widehat{B_1}\)
Mà \(\widehat{B_1}=\widehat{F_1}\)(2 góc so le trong do AB//CD)
\(\Rightarrow\widehat{D_2}=\widehat{F_1}\)
Mà 2 góc này đồng vị
=> DE//BF
b) Xét tứ giác DEBF có:
DE//BF(cmt)
DF//EB(ABCD là hình bình hành)
=> Tứ giác DEBF là hình bình hành
Cho tam giác ABC vuông tại A đường cao AH .Gọi IK theo thứ tự trung điểm của AB,AC chứng minh
a, IH//AC,HK//AB