Các bạn không cần phải vẽ hình đâu chỉ giải là được
1) Cho hình bình hành ABCD, E là điểm trên AB. DE kéo dài cắt đường thẳng BC tại F.
CM: tam giác ABE đồng dạng với tam giác BFE
2) Cho tam giác ABC vuông tại A với AC 3 cm, BC 5cm. Vẽ đường cao AK
Cm: tam giác ABC đồng dạng với tam giác KBA và AB^2BK.BC
3) Cho tam giác ABC có AB 15 cm, AC 20 cm BC 25 cm. Trên cạnh AB lấy điểm E sao cho AE 8 cm, trên cạnh AC lấy F sao cho AF 6 cm
So sánh AE/AC;AF/AB
4) Cho tam giác ABC vuông tại A đ...
Đọc tiếp
Các bạn không cần phải vẽ hình đâu chỉ giải là được
1) Cho hình bình hành ABCD, E là điểm trên AB. DE kéo dài cắt đường thẳng BC tại F.
CM: tam giác ABE đồng dạng với tam giác BFE
2) Cho tam giác ABC vuông tại A với AC = 3 cm, BC = 5cm. Vẽ đường cao AK
Cm: tam giác ABC đồng dạng với tam giác KBA và AB^2=BK.BC
3) Cho tam giác ABC có AB= 15 cm, AC = 20 cm BC = 25 cm. Trên cạnh AB lấy điểm E sao cho AE = 8 cm, trên cạnh AC lấy F sao cho AF = 6 cm
So sánh AE/AC;AF/AB
4) Cho tam giác ABC vuông tại A đường cao AH cắt phân giác BD tại I
Cm IA.BH=IH.BA
5) Cho tam giác nhọn ABC có AB = 12 cm AC = 15 cm. Trên các cạnh AB và AC lấy các điểm D và E sao cho AD = 4 cm AF = 5 cm
Cm DE // BC, Từ đó suy ra tam giác ADE đồng dạng với tam giác ABC
6) tam giác AOB có AB bằng 18 cm OA = 12 cm OB = 9 cm. Trên tia đối của tia OB lấy điểm D sao cho OD = 3 cm. Qua E kẻ đường thẳng song song với AB cắt tia AO ở C. Gọi F là giao điểm của AD và BC
Tính độ dài OC;CD
7) Cho tam giác ABC vuông tại A,D nằm giữa A và C. Kẻ đường thẳng qua D vuông góc với BC tại E và cắt tia BA tại F.
Cm tam giác ADF đồng dạng với tam giác EDC.
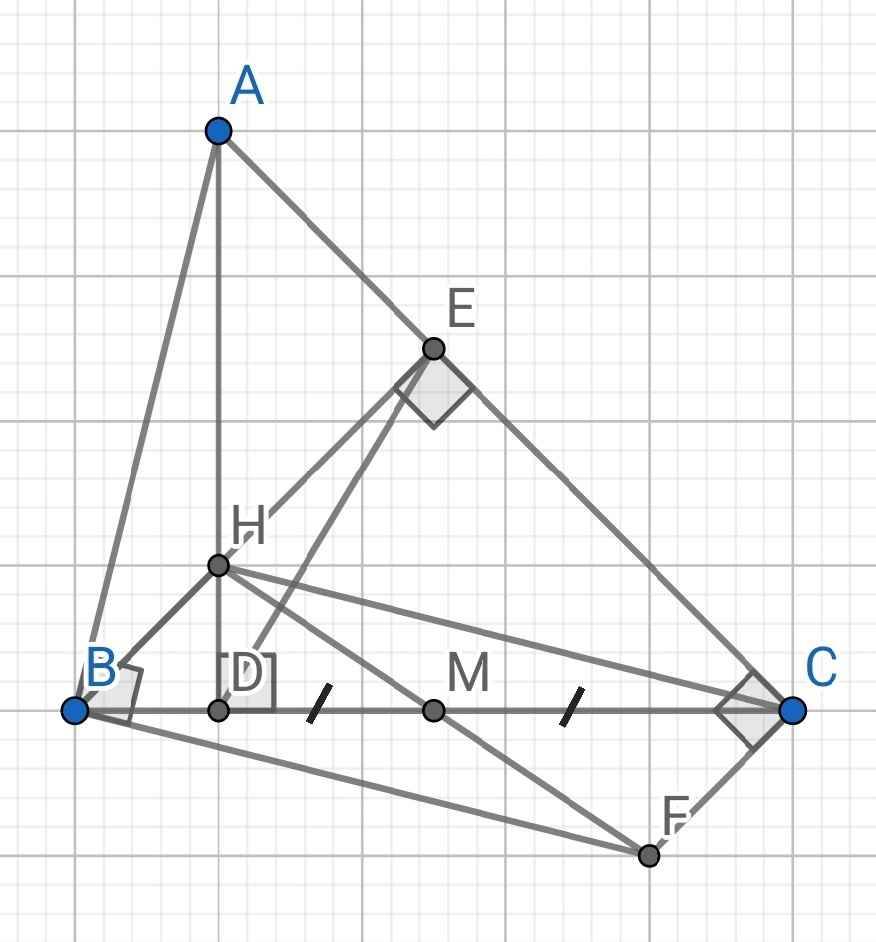 d) Do H là giao điểm của hai đường cao AD và BE của ∆ABC (gt)
d) Do H là giao điểm của hai đường cao AD và BE của ∆ABC (gt)
