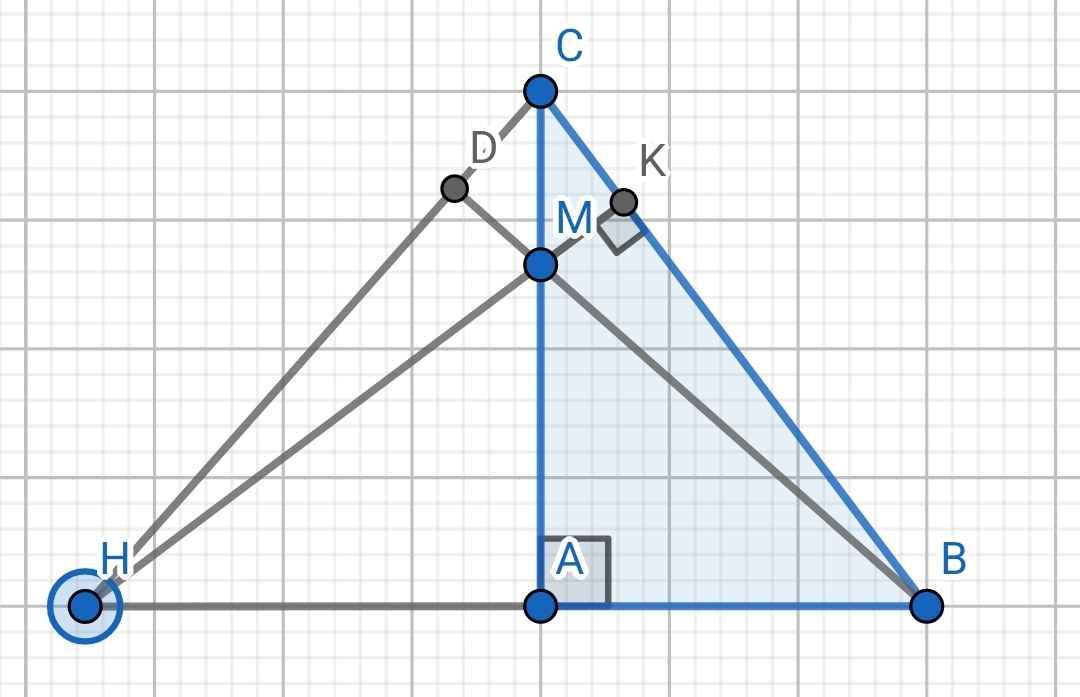
a) Ta có:
∠BMC là góc ngoài của ∆ABM
⇒ ∠BMC = ∠BAM + ∠ABM
⇒ ∠BMC là góc tù nên là góc lớn nhất trong ∆BMC
Mà BC đối diện với ∠BMC nên BC là cạnh lớn nhất
⇒ BC > BM
b) ∆BHC có:
CA ⊥ BH (do CA ⊥ AB) nên CA là đường cao
HK ⊥ BC (do MK ⊥ BC) nên HK là đường cao thứ hai
⇒ BM là đường cao thứ ba (do M là giao điểm của CA và HK)
⇒ BM ⊥ CH


