Question

Cho tam giác ABC vuông tại A, đường cao AH. E, F lần lượt là hình chiếu của H trên AB, AC. Gọi M là trung điểm BC. Chứng minh \(S_{AEMF}=\dfrac{1}{2}S_{ABC}\)

Answer 1

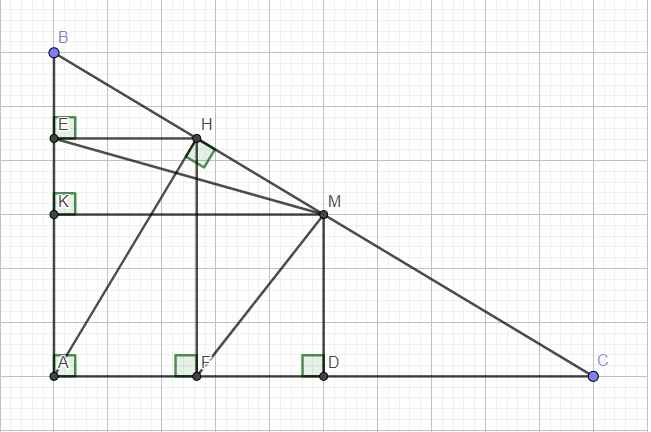
Cái bài này thì có lẽ bạn nên chứng minh AM⊥FE là nó ra liền à

Answer 2

Tứ giác AEHF là hình chữ nhật (3 góc vuông) \(\Rightarrow HE=AF\) và \(AE=HF\)

\(S_{ABC}=S_{ABH}+S_{ACH}=\dfrac{1}{2}HE.AB+\dfrac{1}{2}HF.AC=\dfrac{1}{2}AB.AF+\dfrac{1}{2}AC.AE\)

Gọi K là trung điểm AB \(\Rightarrow MK\) là đường trung bình tam giác ABC \(\Rightarrow\left\{{}\begin{matrix}MK=\dfrac{1}{2}AC\\MK\perp AB\end{matrix}\right.\)

Gọi D là trung điểm AC \(\Rightarrow MD\) là đtb tam giác ABC \(\Rightarrow\left\{{}\begin{matrix}MD=\dfrac{1}{2}AB\\MD\perp AC\end{matrix}\right.\)

\(S_{AEMF}=S_{ABC}-\left(S_{BME}+S_{CMF}\right)=S_{ABC}-\left(\dfrac{1}{2}MK.BE+\dfrac{1}{2}MD.CF\right)\)

\(=S_{ABC}-\dfrac{1}{2}\left(\dfrac{1}{2}AC.\left(AB-AE\right)+\dfrac{1}{2}AB.\left(AC-AF\right)\right)\)

\(=S_{ABC}-\dfrac{1}{2}\left(AB.AC-\left(\dfrac{1}{2}AC.AE+\dfrac{1}{2}AB.AF\right)\right)\)

\(=S_{ABC}-\dfrac{1}{2}\left(2S_{ABC}-S_{ABC}\right)=\dfrac{1}{2}S_{ABC}\) (đpcm)

Answer 3