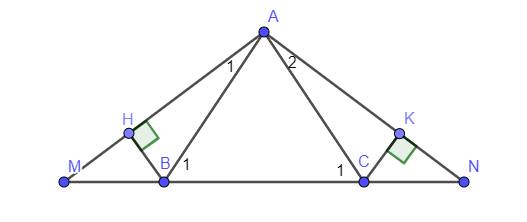
`a)`
Có `Delta ABC` cân tại `A=>hat(B_1)=hat(C_1);AB=AC`
Có `hat(B_1)+hat(ABM)=180^0` ( kề bù )
`hat(C_1)+hat(ACN)=180^0` (kề bù)
mà `hat(B_1)=hat(C_1)(cmt)`
nên `hat(ABM)=hat(ACN)`
Xét `Delta ABM` và `Delta ACN` có :
`AB=C(cmt)`
`hat(ABM)=hat(ACN)(cmt)`
`BM=CN(GT)`
`=>Delta ABM=Delta ACN(c.g.c)(đpcm)`
`b)`
Có `Delta ABM=Delta ACN(cmt)=>hat(A_1)=hat(A_2)` ( 2 góc t/ứng )
Xét `Delta AHB` và `Delta AKC` có :
`hat(AHB)=hat(AHC)(=90^0)`
`AB=AC(cmt)`
`hat(A_1)=hat(A_2)(cmt)`
`=>Delta AHB=Delta AKC(c.h-g.n)(đpcm)`