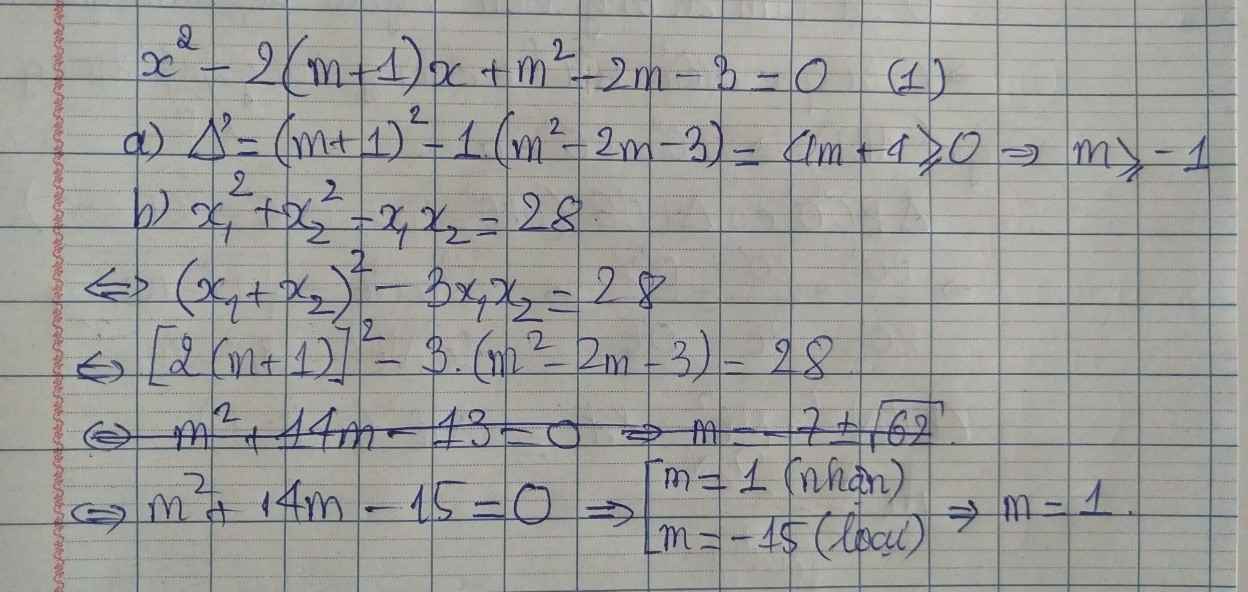a: \(\Delta=\left(2m+2\right)^2-4\left(m^2-2m-3\right)\)
\(=4m^2+8m+4-4m^2+8m+12\)
=16m+16
Để phương trình luôn có nghiệm thì 16m+16>=0
hay m>=-1
b: Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2-x_1x_2=28\)
\(\Leftrightarrow\left(2m+2\right)^2-3\left(m^2-2m-3\right)=28\)
\(\Leftrightarrow4m^2+8m+4-3m^2+6m+9=28\)
\(\Leftrightarrow m^2+14m-15=0\)
=>(m+15)(m-1)=0
=>m=1
Cho phương trình ẩn x: x2 - 2(m+1)x + m2 - 1 = 0 . Tìm giá trị của m để phương tình có 2 nghiệm x1 x2 thỏa mãn x12 + x22 = x1.x2 + 8
Cho pt: x2 - (m + 2) + 7m - 2m2 - 3 = 0 (với x là ẩn số) (1)
a) Chứng tỏ phương trình (1) luôn có 2 nghiệm phân biệt.
b) Tìm m để phương trình (1) có hai nghiệm x1 , x2 thỏa hệ thức:
2(x12 - x22) - 5x1x2 = 2
Cho phương trình x2 + 2mx – 1 = 0 ( m là tham số ) (2)
a/ Chứng minh phương trình(2) luôn có hai nghiệm phân biệt với mọi m
b/ Gọi x1, x2 là hai nghiệm của phương trình trên, tìm m để x12 + x22 – x1x2 = 7
Cho phương trình 4x2-2(2m+3)x+m+1=0
a) với giá trị nào của m thì phương trình có một nghiệm bằng 0, tìm nghiệm còn lại
b) Trong trường hợp phương trình có 2 nghiệm x1 và x2, tìm tất cả các giá trị của m để (x1+x2) / (x1x2) < 4
MONG NHẬN ĐƯỢC SỰ GIÚP ĐỠ TỪ CÁC CAO NHÂN !!!
1. Cho phương trình: x2 – 2(2m – 1)x + 8m - 8 = 0.(1)
a) Giải (1) khi m = 2.
b, Tìm m để phương trình có hai nghiệm phân biệt
c) Tìm m để phương trình có hai nghiệm x1, x2 thỏa mãn A = 
đạt giá trị nhỏ nhất
Cho phương trình x2+ 2(m − 1)x − 6m − 7 = 0 (1) (m là tham số).
a) Chứng minh rằng với mọi giá trị của m thì phương trình (1) luôn có hai nghiệm phân biệt.
b) Gọi x1, x2là hai nghiệm của phương trình (1). Tìm các giá trị của m thỏa x1(x1+3/3x2)+x2(x2+3/2x1)=15
các bạn ai biết thì chỉ giúp mình với ạ
Cho phương trình: x2 - 3x - m2 + m + 2 = 0 (1)
Tìm m để pt(1) có 2 nghiệm phân biệt x1,x2 sao cho: x12 + x22 = 5
cho phương trình x2+(m-3)x-m+1=0
A)tìm m để phương trình có 2 no x1,x2 sao cho P=x1x2-x21-x22 đạt giá trị lớn nhất
B)tìm m để phương trình có 2no x1,x2 cho bt T=15/(x1-3x2)x1+x22 đạt giá trị lớn nhất
3x2 là x2 ko phải là mũ 2 ạ ở phần này ko có mũ 2 ạ
X22 cái nào em viết trc là ở trên ạ
Em cảm ơn ạ
cho phương trình x² - 2(m+1)x +m² +4 = 0 . tìm m để phương trình có hai nghiệm x1 x2 sao cho C = x1 +x2 - x1x2 +3 đạt giá trị lớn nhất và tìm giá trị lớn nhất đó
