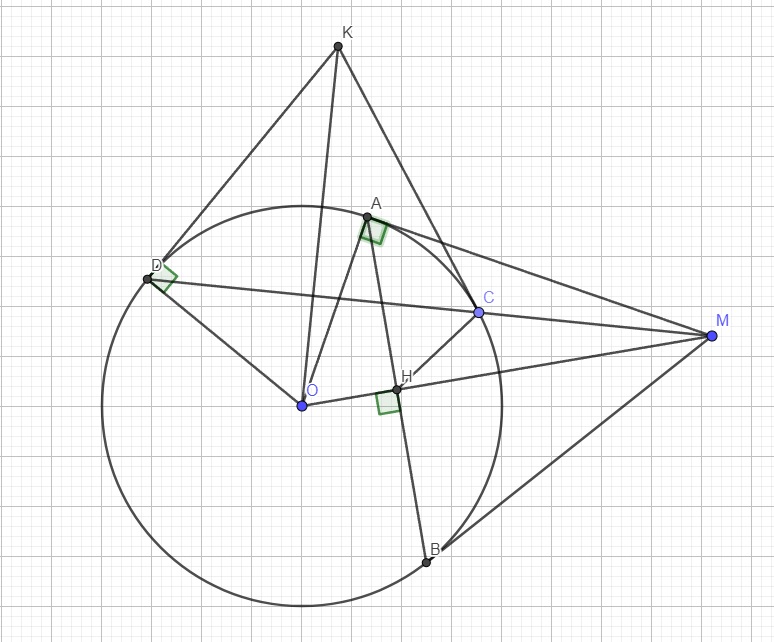
Gọi H là giao điểm OM và BC
Ta có: \(MA=MB\) (t/c hai tt cắt nhau), \(OA=OB=R\)
\(\Rightarrow OM\) là trung trực AB
\(\Rightarrow OM\perp AB\) tại H (1)
\(\widehat{MDA}=\widehat{MAC}\) (cùng chắn AC) và \(\widehat{AMC}\) là góc chung nên \(\Delta MAC\sim\Delta MDA\left(g.g\right)\)
\(\Rightarrow\dfrac{MA}{MD}=\dfrac{MC}{MA}\Rightarrow MA^2=MD.MC\)
Trong tam giác vuông OAM với đường cao AH, áp dụng hệ thức lượng:
\(MA^2=MH.MO\)
\(\Rightarrow MD.MC=MH.MO\Rightarrow\dfrac{MC}{MO}=\dfrac{MH}{MD}\)
Lại có góc \(\widehat{CMH}\) chung \(\Rightarrow\Delta MCH\sim\Delta MOD\left(c.g.c\right)\)
\(\Rightarrow\widehat{MHC}=\widehat{MDO}\)
Mà \(\widehat{MHC}+\widehat{CHO}=180^0\Rightarrow\widehat{MDO}+\widehat{CHO}=180^0\)
\(\Rightarrow CDHO\) nội tiếp (2)
KC, KD là tiếp tuyến nên \(\widehat{OCK}=\widehat{ODK}=180^0\Rightarrow ODKC\) nội tiếp đường tròn đường kính OK (3)
(2);(3)\(\Rightarrow\)H thuộc đường tròn đường kính OK
\(\Rightarrow\widehat{KHO}=90^0\) (góc nt chắn nửa đường tròn)
\(\Rightarrow KH\perp OM\) tại H (4)
(1);(4) \(\Rightarrow K;A;B\) thẳng hàng
//Đây chắc là câu cuối trong 1 bài hình nhiều ý. Lần sau em lưu ý nên đưa hết đề lên (chỗ nào ko cần làm thì ghi vô), để rất nhiều thứ mọi người đỡ phải chứng minh lại từ đầu mà sử dụng luôn kết quả có sẵn từ các ý trước.