AB bằng bao nhiêu vậy bạn?
\(S=\dfrac{4}{3}\pi R^3=288\pi\Rightarrow R=6\)
\(AB=6\)
Áp dụng định lý Pitago:
\(d\left(O;AB\right)=\sqrt{R^2-\left(\dfrac{AB}{2}\right)^2}=\sqrt{6^2-3^2}=3\sqrt{3}\)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
AB bằng bao nhiêu vậy bạn?
\(S=\dfrac{4}{3}\pi R^3=288\pi\Rightarrow R=6\)
\(AB=6\)
Áp dụng định lý Pitago:
\(d\left(O;AB\right)=\sqrt{R^2-\left(\dfrac{AB}{2}\right)^2}=\sqrt{6^2-3^2}=3\sqrt{3}\)
cho mặt cầu (s) tâm o và có thể tích là 288π. mặt phẳng (P) cắt (S) tại (C) và khoảng cách từ tâm (S) đến (P) là 2 căn 5 thì bán kính của đường tròn (C) là
cho mặt cầu (S) tâm O và có thể tích là 288π. diện tích đường tròn lớn nhất của (S) là
Cho mặt cầu (S) tâm O bán kính R và một đường thẳng d. Kí hiệu h là khoảng cách từ O đến đường thẳng d. Đường thẳng d có điểm chung với mặt cầu (S) nếu và chỉ nếu:
A. h ≤ R
B. h = R
C. h > R
D. h < R
Cho mặt cầu (S) có tâm O và bán kính R biết diện tích của (S) là 36π. Hai điểm A,B thuộc (S) và khoảng cách từ O đến AB là 2 căn 2 Tính AB
Cho mặt cầu (S) tâm O, bán kính R = 3. Mặt phẳng (P) cách O một khoảng bằng 1 và cắt (S ) theo giao tuyến là đường tròn (C) có tâm H . Gọi T là giao điểm của tia OH và (S) , tính thể tích V của khối nón có đỉnhT và đáy là hình tròn (C ).
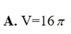
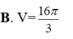
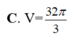
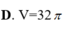
Cho mặt cầu (S) tâm O và các điểm A, B, C nằm trên mặt cầu (S) sao cho AB=3, AC=4, BC=5 và khoảng cách từ O đến mặt phẳng (ABC) bằng 1. Thể tích của khối cầu (S) bằng
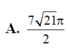
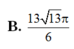
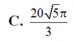
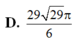
Cho mặt cầu (S) tâm O, bán kính bằng 2. (P) là mặt phẳng cách O một khoảng bằng 1 và cắt (S) theo một đường tròn (C). Hình nón (N) có đáy là (C), đỉnh thuộc (S), đỉnh cách (P) một khoảng lớn hơn 2. Kí hiệu V 1 , V 2 lần lượt là thể tích của khối cầu (S) và khối nón (N). Tỉ số V 1 V 2 là
![]()
![]()
![]()
![]()
Cho đường thẳng d : x + 5 2 = y - 7 - 2 = z 1 và điểm I ( 4 ; 1 ; 6 ) . Đường thẳng d cắt mặt cầu (S) có tâm I, tại hai điểm A, B sao cho A B = 6 . Phương trình của mặt cầu (S) là:
A. x - 4 2 + y - 1 2 + z - 6 2 = 18
B. x + 4 2 + y + 1 2 + z + 6 2 = 18
C. x - 4 2 + y - 1 2 + z - 6 2 = 9
D. x - 4 2 + y - 1 2 + z - 6 2 = 16
Trong không gian cho đường thẳng Δ và điểm O cách Δ một khoảng bằng 20cm. Mặt cầu (S) tâm O cắt đường thẳng Δ theo một dây có độ dài 30cm có bán kính r bằng:
A. r = 45cm
B. r = 30cm
C. r = 25cm
D. r = 20cm