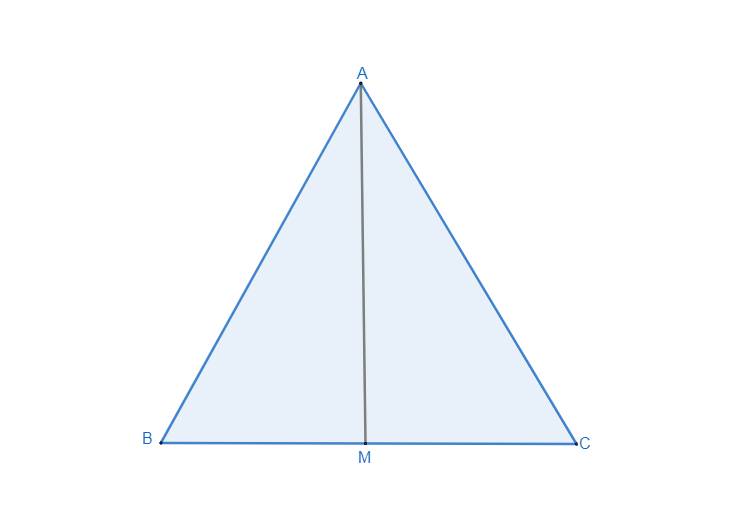
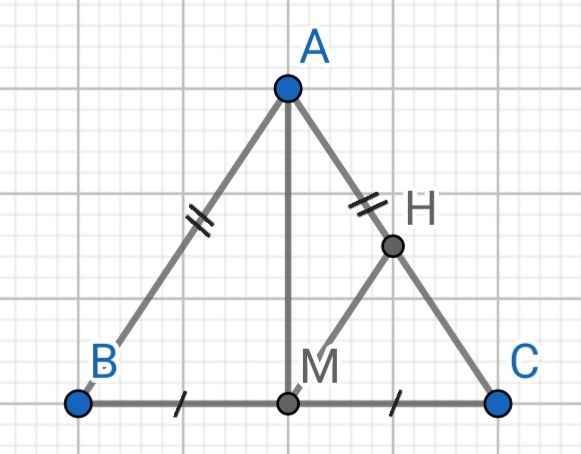
 a) Xét ∆AMB và ∆AMC có:
a) Xét ∆AMB và ∆AMC có:
AB = AC (gt)
AM là cạnh chung
MB = MC (do M là trung điểm của BC)
⇒ ∆AMB = ∆AMC (c-c-c)
b) Do ∆AMB = ∆AMC (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
c) Do ∆AMB = ∆AMC (cmt)
⇒ ∠ABM = ∠ACM (hai góc tương ứng)
⇒ ∠ABM = ∠HCM (1)
Do MH // AB (gt)
⇒ ∠ABM = ∠HMC (đồng vị) (2)
Từ (1) và (2) ⇒ ∠HMC = ∠HCM
Do ∆AMB = ∆AMC (cmt)
⇒ ∠MAB = ∠MAC (hai góc tương ứng)
⇒ ∠MAB = ∠HAM (3)
Do MH // AB (gt)
⇒ ∠MAB = ∠HMA (so le trong) (4)
Từ (3) và (4) ⇒ ∠HMA = ∠HAM