Giải:
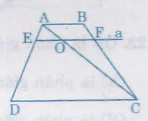
a) Nối AC cắt EF tại O
∆ADC có EO // DC => = (1)
∆ABC có OF // AB => = (2)
Từ 1 và 2 => =
b) Từ = => =
hay =
c) Từ = => =
Đúng 0
Bình luận (0)
1. Cho hình thang ABCD (AB//CD). Đường thẳng a song song với DC, cắt các cạnh AD và BC theo thứ tự tại M và N.
Chứng minh rằng: a) \(\dfrac{AM}{MD}=\dfrac{BN}{NC};\) b)\(\dfrac{AM}{AD}=\dfrac{BN}{BC};\) c)\(\dfrac{DM}{DA}=\dfrac{CN}{CB}.\)
2. Cho hình thang ABCD (AB // CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh bên AD, BC theo thứ tự tại E và F (h.24).
So sánh OE và OF.
Cho hình thang ABCD ( AB//CD) . Kẻ đường thẳng a song song với DC, cắt AD tại M và cắt BC tại N. Chứng minh rằng:
a) \(\dfrac{AM}{MD}\)= \(\dfrac{BN}{NC}\)
b) \(\dfrac{AM}{AD}\)=\(\dfrac{BN}{BC}\)
c)\(\dfrac{DM}{DA}\)=\(\dfrac{CN}{CB}\)
Cho hình thang ABCD (AB//CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh bên AD, BC theo thứ tự tại E và F (h.26)
Chứng minh rằng OE = OF
Cho \(\Delta ABC\) có BC = a, AC = B, AB = c. Các đường phân giác AD, BE, CF cắt nhau tại I. Chứng minh:
a. \(\dfrac{DI}{DA}=\dfrac{a}{a+b+c}\) b. \(\dfrac{DI}{DA}+\dfrac{EI}{EB}+\dfrac{EI}{FC}=1\)
Cho hình bình hành ABCD. Đường phân giác góc A cắt BD tại E, đường phân giác góc B cắt AC tại F. Chứng minh:
a) \(\dfrac{BE}{ED}=\dfrac{AF}{FC}\)
b) EF//AB
Cho \(\Delta\)ABC có AD là đường phân giác trong \(\widehat{BAC}\), D \(\in\) BC. Qua D kẻ đường thẳng song song với AC, cắt AB tại E. CMR:
\(\dfrac{1}{AB}+\dfrac{1}{AC}=\dfrac{1}{AE}\)
1, Qua trọng tâm G của tam giác ABC, kẻ đường thẳng song song với AC, cắt AB và BC lần lượt ở D và E. Tính độ dài đoạn DE, biết AD + EC = 16cm, chu vi tam giác ABC = 75cm.
2, Cho hình thang ABCD(AB//CD). Đường thẳng song song hai đáy cắt cạnh AD tại M, cắt cạnh BC tại N sao cho MD = 3 MA.
a, Tính tỉ số \(\dfrac{NB}{NC}\)
b, Cho AB = 8cm, CD = 20cm. Tính MN.
3, Cho tam giác ABC> Trên các cạnh AB, AC lần lượt lấy các điểm B', C' sao cho \(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}.\) Qua B' vẽ đường thẳng a song song với Bc, cắt cạnh AC tại C''.
a, So sánh độ dài các đoạn thẳng AC' và AC''.
b, Chứng minh B'C' // BC.
4, Cho tam gác ABC. Gọi D là điểm chia cạnh AB thàng hai đoạn thẳng có độ dài AD = 13,5cm; DB = 4,5cm. Tính tỉ số các khoảng cách từ các điểm D và B đến cạnh AC.
MỘI NGƯỜI KẺ HÌNH GIÚP MK LUÔN NHÁ !!!
MƠN ẠK
Cho hình thang ABCD (AB // CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự tại E và F.Chứng minh rằng OE = OF
Cho hình thang ABCD, đáy nhỏ CD. Từ D kẻ đường thẳng song song với BC, cắt AC tại M, cắt AB tại K. Từ C kẻ đường thẳng song với AD, cắt AB tại F. Qua F kẻ đường thẳng song song với AC cắt BC tại P. Chứng minh rằng:
a) Các tứ giác AFCD, DCBK là hình bình hành.
b) MP // AB.
c) Ba đường thẳng MP, CF, DB đồng qui.