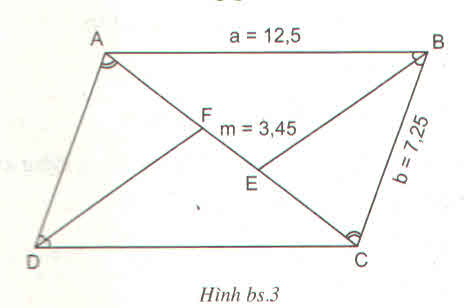
Lời giải:
a) Theo tính chất đường phân giác ta có:
$\frac{BE}{ED}=\frac{AB}{AD}$
$\frac{AF}{FC}=\frac{AB}{BC}$
Mà $ABCD$ là hình bình hành nên $AD=BC\Rightarrow \frac{AB}{AD}=\frac{AB}{BC}$
$\Rightarrow \frac{BE}{ED}=\frac{AF}{FC}$ (đpcm)
b) Gọi O là giao điểm $AC,BD$. Ta có:
\(\frac{BE}{ED}=\frac{BD-ED}{ED}=\frac{2DO-ED}{ED}=\frac{2DO}{ED}-1\)
Tương tự: \(\frac{AF}{FC}=\frac{2OC}{FC}-1\)
Mà \(\frac{BE}{ED}=\frac{AF}{FC}\Rightarrow \frac{DO}{ED}=\frac{OC}{FC}\). Theo định lý Talet đảo suy ra $EF\parallel DC$ hay $EF\parallel AB$ (đpcm)