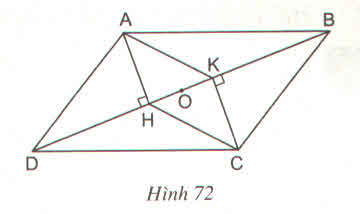
Xét ΔADH và ΔCBK lần lượt vuông tại H và K có:
AD=BC(tứ giác ABCD là hình bình hành)
\(\widehat{ADH}=\widehat{CBK}\) (2 góc so le trong do AD//BC)
=>ΔADH=ΔCBK(ch-gn)
=>DH=BK
Mà OH=OK(O là trung điểm HK)
=> DH+OH=BK+OK
=> DO=OB
=> O là trung điểm BD
=> O là giao điểm 2 đường chéo AC, BD của hình hình hành ABCD
=> A,O,C thẳng hàng
AHCK là HBH =>2 đường chéo AC và HK cắt nhau tại trung điểm của mỗi đường
Mà O là trung điểm của HK
=> O là trung điể của AC
=> A,O,C thẳng hàng
b: Xét ΔADH vuông tại H và ΔCBK vuông tại K có
AD=CB
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔADH=ΔCBK
Suy ra: AH=CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành
Suy ra: Hai đường chéo AC và HK cắt nhau tại trung điểm của mỗi đường
mà O là trung điểm của HK
nên O là trung điểm của AC
hay A,O,C thẳng hàng