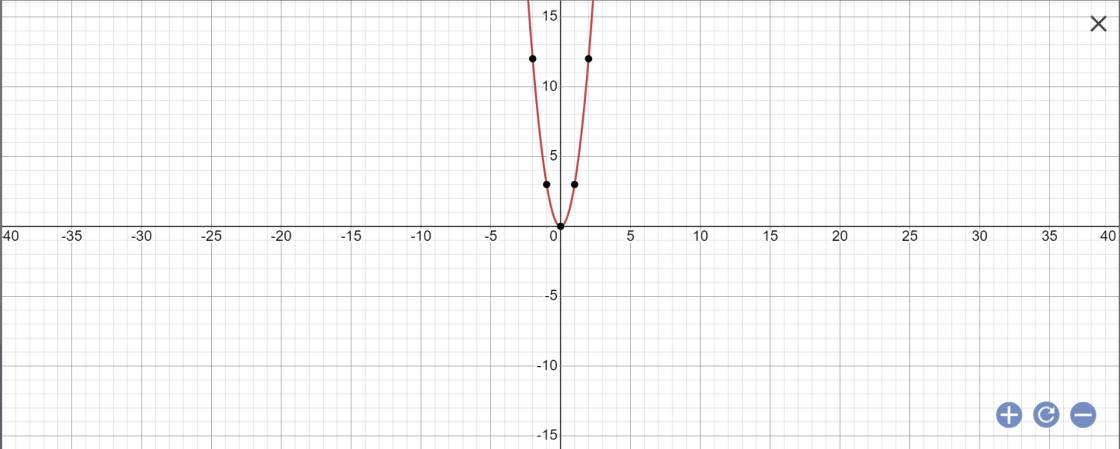
a: f(x)=3x^2
a=3>0
=>Hàm số đồng biến khi x>0 và nghịch biến khi x<0
b: f(1)=f(-1)=3*1^2=3
f(2)=3*2^2=12
f(-4)=3*(-4)^2=48
c: f(x)=48
=>x^2=48/3=16
=>x=4 hoặc x=-4
d; 
Tìm x để biểu thức sau có nghĩa:
c) \(\dfrac{1}{\sqrt{4x^2-12x+9}}\)
d) \(\dfrac{1}{\sqrt{x^2-x+1}}\)
e) \(\dfrac{1}{\sqrt{x^2-8x+15}}\)
f) \(\dfrac{1}{\sqrt{3x^2-7x+20}}\)
Với giá trị nào của x thì các căn thức trên có nghĩa :
a)\(\sqrt{3x^2+1}\)
b)\(\sqrt{4x^2-4x+1}\)
c)\(\sqrt{\dfrac{3}{x+4}}\)
h)\(\sqrt{x^2-4}\)
i) \(\sqrt{\dfrac{2+x}{5-x}}\)
Rút gọn:
a, A = \(\sqrt{\left(1-x\right)^2}-1\) với x < 1
b, B = \(\frac{3-\sqrt{x}}{x-9}\) với x ≥ 0 và x ≠ 9
c, C = \(\frac{x-5\sqrt{x}+6}{\sqrt{x}-3}\) với x ≥ 0 và x ≠ 9
d, D = 5 - 3x - \(\sqrt{25-10x+x^2}\) với x < 5
e, E = \(\sqrt{3a}.\sqrt{27a}\) với a ≥ 0
f, F = \(\frac{1}{a-1}\sqrt{9\left(a-1\right)^2}\) với a > 1
√x+2 có nghĩa khi
Trong các biểu thức dưới đây, biểu thức nào được xác định với mọi số thực x?
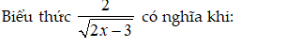
giúp mình với
cho (O), dây AB không qua tâm và C là điểm chính giữa cung nhỏ AB. Gọi D là điểm bất kì thuộc tia đối của tia BA. Qua D kẻ các đường thẳng song song với BC và AC, chúng lần lượt cắt các đường thẳng AC và BC tại E và F a) Chứng minh CE=DF=BF b) chứng minh 4 điểm O,C,E,F cùng thuộc một đường tròn c) Gọi K là giao điểm thứ hai của đường tròn (O) và đường tròn đi qua 4 điểm O,C,E,F. Chứng minh CK vuông góc với KD
tìm a để biểu thức có nghĩa:
a) \(\sqrt{\dfrac{-a}{3}}\)
b) \(-\sqrt{\dfrac{1}{a^2}}\)
c) \(\sqrt{\dfrac{\left(1-a\right)^3}{a^2}}\)
d) \(\sqrt{\dfrac{a^{2^{ }}+1}{1-2a}}\)
e) \(\sqrt{a^2-1}\)
f) \(\sqrt{\dfrac{2a-1}{2-a}}\)
Tìm điều kiện có nghĩa của các căn thức sau:
a) \(\sqrt{3x-2}\) b) \(\sqrt{4-2x}\) c) \(\sqrt{-4x}\)
d)\(\sqrt{x^2-2x+1}\) e) \(\sqrt{\dfrac{x^2+1}{3-2x}}\) f) \(\sqrt{-15+8x-x^2}\)
Bài tập: Cho hàm số y=-\(\dfrac{1}{2}\)x2
a, Trên (P) lấy 2 điểm M và N lần lượt có hoành độ là -2 ; 1. Viết ptđt MN.
b, Xác định hàm số y=ax+b biết rằng đt (D) của nó song song với đt MN và chỉ cắt (P) tại 1 điểm.
1 ,Với a < 0 thì số nào lớn hơn trong hai số \(\sqrt{-a}\) và \(\sqrt{-2a}\)
2, Giải các phương trình
a, \(^{3x^2=0,75}\) b,\(2\sqrt{3x}=12\)
c, \(5x^2=80\) d, \(\sqrt{3x\le6}\)
3, Tìm số x không âm , biết \(\frac{1}{2}\sqrt{5x}< 10\)
4, Tính tổng có giá trị của x thỏa mãn đẳng thức \(\sqrt{x^2+25=13}\)
