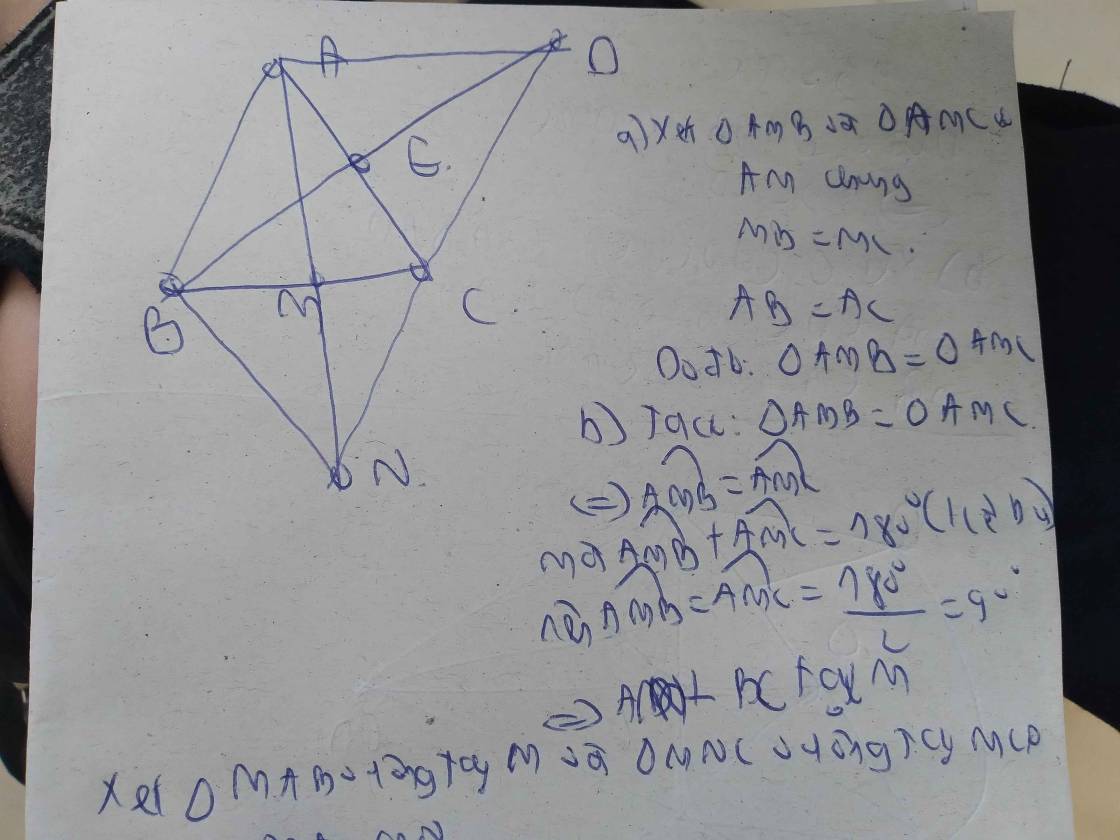
a) Do M là trung điểm của BC (gt)
⇒ BM = MC
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆ABM và ∆ACM có:
AB = AC (cmt)
AM là cạnh chung
BM = MC (cmt)
⇒ ∆ABM = ∆ACM (c-c-c)
b) Xét ∆ABM và ∆NCM có:
AM = MN (gt)
∠AMB = ∠NMC (đối đỉnh)
BM = MC (cmt)
⇒ ∆ABM = ∆NCM (c-g-c)
⇒ ∠ABM = ∠NCM (hai góc tương ứng)
Mà ∠ABM và ∠NCM là hai góc so le trong
⇒ AB // NC
c) Do E là trung điểm của AC (gt)
⇒ AE = CE
Xét ∆ABE và ∆CDE có:
AE = CE (cmt)
∠AEB = ∠CED (đối đỉnh)
BE = ED (gt)
⇒ ∆ABE = ∆CDE (c-g-c)
⇒ ∠BAE = ∠DCE (hai góc tương ứng)
Mà ∠BAE và ∠DCE là hai góc so le trong
⇒ AB // CD
Lại có AB // NC (cmt)
⇒ N, C, D thẳng hàng (1)
Do ∆ABE = ∆CDE (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Do ∆ABM = ∆NCM (cmt)
⇒ AB = NC (hai cạnh tương ứng)
Mà AB = CD (cmt)
⇒ NC = CD (2)
Từ (1) và (2) ⇒ C là trung điểm của ND