Question

Cho ΔABC cân tại A, đường phân giác góc ABC cắt cạnh AC tại D và cho biết AB = 15 cm, BC = 10 cm

a) Tính AD, DC

b) Đường vuông góc với BD tại B cắt đường thẳng AC kéo dài tại E. Tính EC

Giúp e với ạ, e cảm ơn.

Answer 1

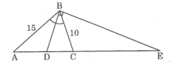
a: Xét ΔABC có BD là phân giác

nên \(\dfrac{AD}{AB}=\dfrac{DC}{BC}\)

=>\(\dfrac{AD}{15}=\dfrac{DC}{10}\)

=>\(\dfrac{AD}{3}=\dfrac{DC}{2}\)

mà AD+DC=AC=15cm

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{AD}{3}=\dfrac{DC}{2}=\dfrac{AD+DC}{3+2}=\dfrac{15}{5}=3\)

=>\(\left\{{}\begin{matrix}AD=3\cdot3=9\left(cm\right)\\DC=2\cdot3=6\left(cm\right)\end{matrix}\right.\)

b: Xét ΔABC có

BD là phân giác trong tại đỉnh B

BE\(\perp\)BD tại B

Do đó: BE là phân giác ngoài tại đỉnh B của ΔABC

Xét ΔABC có BE là phân giác ngoài tại đỉnh B

nên \(\dfrac{EC}{EA}=\dfrac{BC}{BA}\)

=>\(\dfrac{EC}{EC+CA}=\dfrac{10}{15}=\dfrac{2}{3}\)

=>\(\dfrac{EC}{EC+15}=\dfrac{2}{3}\)

=>3EC=2EC+30

=>EC=30(cm)