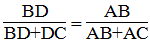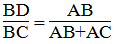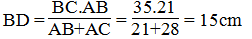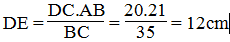Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2=AB2+AC2=212+282=1225BC2=AB2+AC2=212+282=1225
Suy ra: BC = 35 (cm)
Vì AD là đường phân giác của ∠∠(BAC) nên:
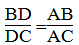
Suy ra:
Hay
Suy ra:
Vậy DC = BC – BD = 35 – 15 = 20cm
Trong ΔABC ta có: DE // AB
Suy ra: 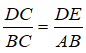
Suy ra:
Đúng 2
Bình luận (0)
a: BC=35(cm)
Xét ΔABC có AD là đường phân giác
nên BD/AB=CD/AC
hay BD/21=CD/28
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{21}=\dfrac{CD}{28}=\dfrac{BD+CD}{21+28}=\dfrac{35}{49}=\dfrac{5}{7}\)
Do đó: BD=15(cm); CD=20(cm)
Xét ΔABC có ED//AB
nên ED/AB=CD/CB
=>ED/21=20/35=4/7
=>ED=12(cm)
Đúng 0
Bình luận (0)