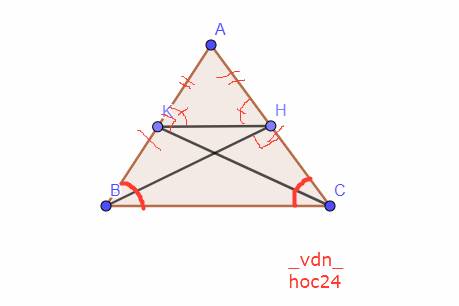
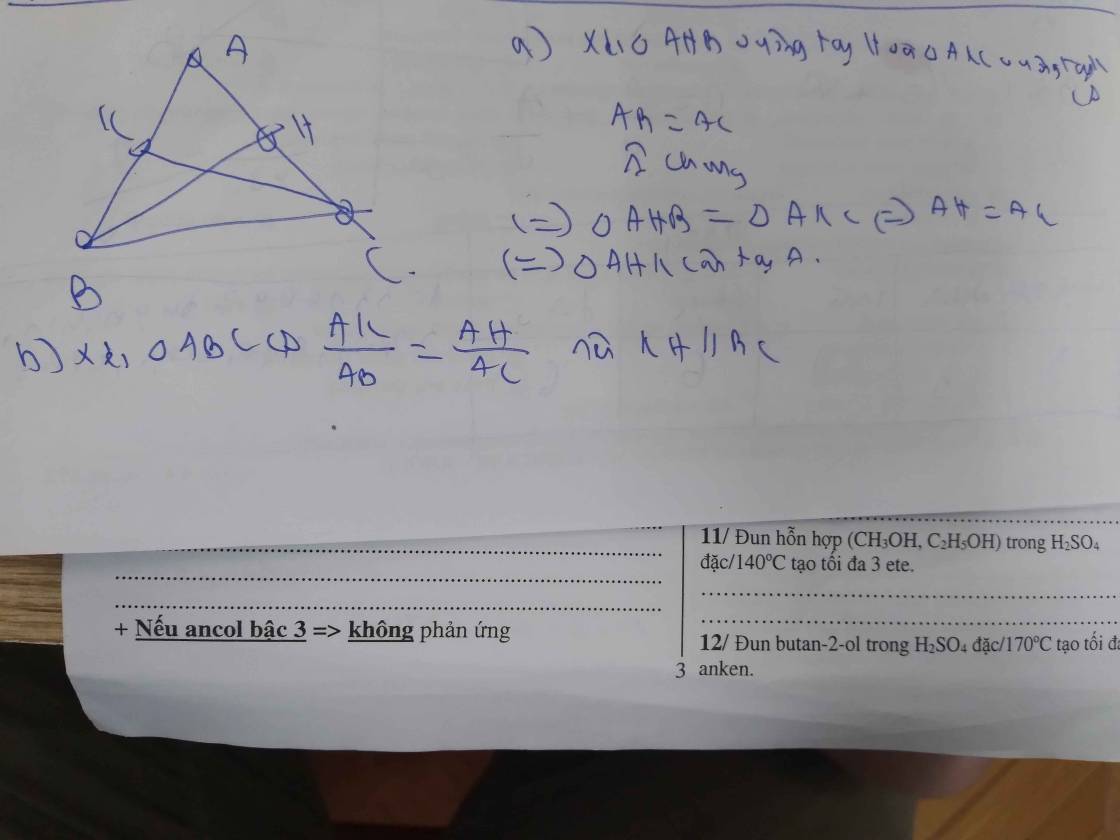
Mình xp sửa đề: Chứng minh: ∆BHA = ∆CKA. Từ đó suy ra ∆AHK cân.
`a,`
Xét Tam giác `BHC` và Tam giác `CKA` có:
\(\widehat{A} \) \(\text{chung}\)
\(AB=AC (\text {Tam giác ABC cân tại A})\)
\(\widehat{AHB}=\widehat{AKC}=90^0\)
`=> \text {Tam giác BHA = Tam giác CKA (ch-gn)}`
`-> AH=AK (\text {2 cạnh tương ứng})`
Xét Tam giác `AHK: AH = AK`
`-> \text {Tam giác AHK cân tại A}`
`b,` Vì Tam giác `AHK` cân tại `A ->`\(\widehat{AKH}=\widehat{AHK}\)
`->`\(\widehat{AHK}=\widehat{AKH}=\)\(\dfrac{180-\widehat{A}}{2}\)
Tam giác `ABC` cân tại `A ->`\(\widehat{ABC}=\widehat{ACB}\)
`->`\(\widehat{ABC}=\widehat{ACB}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{AKH}=\widehat{ABC}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {HK // BC (t/c đt' //)}`