Question

Bài 8: Hãy chỉ ra các cặp tam giác bằng nhau trong  và cho biết chúng bằng nhau theo trường hợp nào.

Answer 1

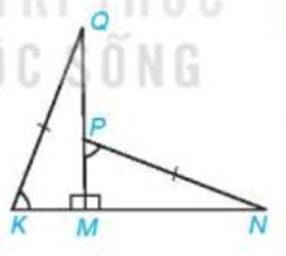
xét tam giác MKQ và tam giác MPN có

góc QMN = góc PMN = 90 độ

góc K = góc MPN (gt)

QK=PN (gt)

Suy ra tam giác MKQ = tam giác MPN (cạnh huyền - góc nhọn)

Answer 2

\(\Delta KMQ=\Delta PMN\left(g.c.g\right)\)

Answer 3

∆MKQ = ∆MPN (g-c-g) vì:

∠MKP = ∠MPN (gt)

KQ = PN (gt)

∠MQK = 180⁰ - (90⁰ + ∠MKP)

= 180⁰ - (90⁰ + ∠MPN)

= ∠MNP

Answer 4

\(\text{#TNam}\)

Xét Tam giác `KQM` và Tam giác `PNM` có:

`KQ=PN`

\(\widehat{K}=\widehat{P}\) 

\(\widehat{KMQ}=\widehat{PMN}=90^0\)

`=>` Tam giác `KQM =` Tam giác `PNM (ch-gn)`