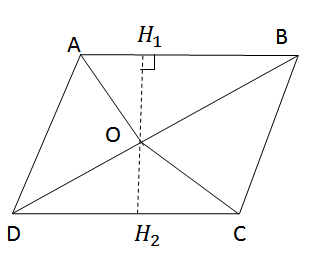
Từ O lẻ đường thẳng d vuông góc với AB ở H1, cắt CD ở H2.
Ta có OH1 ⊥ AB
Mà AB // CD
Nên OH2 ⊥ CD
Do đó :
SABO+ SCDO= \(\frac{1}{2}\)OH1.AB+\(\frac{1}{2}\)OH2.CD = \(\frac{1}{2}AB\left(OH_1+OH_2\right)\) = \(\frac{1}{2}AB.H_1H_2\)
Nên SABO+ SCDO = \(\frac{1}{2}\)SABCD (1)
Tương tự SBCO + SDAO = \(\frac{1}{2}S_{ABCD}\) (2)
Từ (1) và (2) suy ra :
SABO + SCDO = SBCO + SDAO
