Bài 8. Cho AABC vuông tại A có AB = 5cm; BC = 13cm; AH là đường cao. a) Tính AC, AH và B ( Số đo góc làm tròn đến độ, độ dài cạnh làm tròn đến chữ số thì phân thứ hai ). b) Gọi E, F lần lượt là hình chiếu của H trên AB, AC. Chứng minh AE.EB+AF.FC- HB.HC=0 c) Chứng minh AH=EF. Từ đó suy ra BC =3AH + BE +CF.
a) Ta có :
\(BC^2=AB^2+AC^2\left(Pitago\right)\)
\(\Leftrightarrow AC^2=BC^2-AB^2=169-25=144\)
\(\Leftrightarrow AC=12\left(cm\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{AB^2.+AC^2}{AB^2.AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{BC^2}{\left(AB.AC\right)^2}\)
\(\Leftrightarrow AH^2=\dfrac{\left(AB.AC\right)^2}{BC^2}=\dfrac{\left(5.12\right)^2}{13^2}\)
\(\Leftrightarrow AH=\dfrac{5.12}{13}=\dfrac{60}{13}\sim4,85\left(cm\right)\)
\(sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{12}{13}\Rightarrow\widehat{B}\sim67^o\)
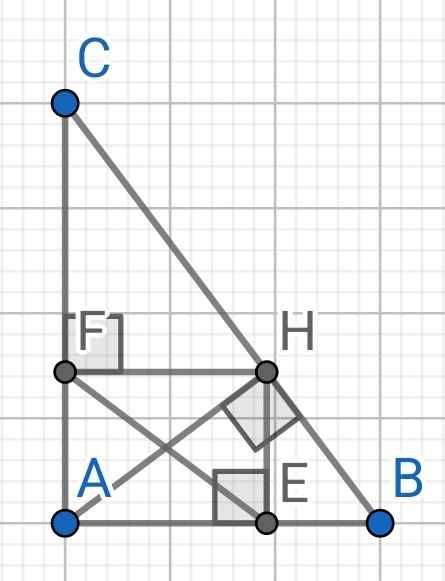 a) ∆ABC vuông tại A (gt)
a) ∆ABC vuông tại A (gt)
BC² = AB² + AC² (Pytago)A
⇒ AC² = BC² - AB²
= 13² - 5²
= 144
⇒ AC = 12 (cm)
Ta có:
AH.BC = AB.AC
⇒ AH = AB.AC : BC
= 5.12 : 13
= 60/13 (cm) ≈ 4,62 (cm)
sinB = AC/BC = 12/13
⇒ ∠B ≈ 67⁰
b) ∆AHB vuông tại H có HE là đường cao
⇒ HE² = AE . EB (1)
∆AHC vuông tại H có HF là đường cao
⇒ HF² = AF . FC (2)
Tứ giác AEHF có:
∠AEH = ∠EAF = ∠AFH = 90⁰
⇒ AEHF là hình chữ nhật
⇒ AH = EF
⇒ ∠EHF = 90⁰
∆EHF vuông tại H
⇒ EF² = HE² + HF²
⇒ AH² = HE² + HF²
Từ (1) và (2)
⇒ AE.EB + AF.FC = HE² + HF² = AH²
∆ABC vuông tại A vó AH là đường cao
⇒ AH² = HB.HC
⇒ AE.EB + AF.FC = HB.HC
⇒ AE.EB + AF.FC - HB.HC = 0
c) AH = EF đã chứng minh ở câu b




