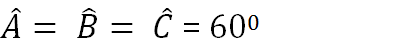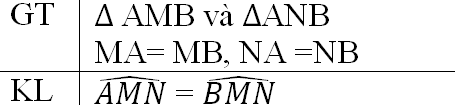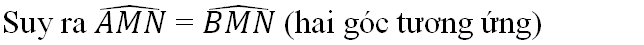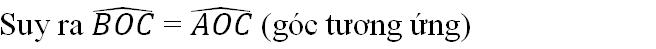bài 15 :
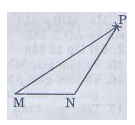
- Vẽ đoạn thẳng MN = 2,5cm.
- Trên cùng một nửa mặt phẳng bờ MN vẽ cung tròn tâm M bán kính 5cm, và cung tròn tâm N bán kính 3cm
- Hai cung tròn cắt nhau tại P. Vẽ các đoạn thẳng MP, NP ta được tam giác MNP.
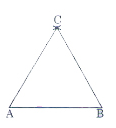
Vẽ tam giác ABC (tương tự với cách vẽ ở Bài 15):
- Vẽ cạnh AB có độ dài bằng 3 cm.
- Trên một nửa mặt phẳng bờ AB lần lượt vẽ hai cung tròn tại A và B có bán kính 3 cm
- Hai cung tròn này cắt nhau tại C. Nối các điểm A, B, C ta được tam giác ABC cần vẽ.
Đo mỗi góc của tam giác ABC ta được:
Hình 68
Xét tam giác ABC và tam giác ABD có:
AB = AB (cạnh chung)
AC = AD (gt)
BC = BD (gt)
Vậy ΔABC = ΔABD (c.c.c)
- Hình 69
Xét tam giác MNQ và tam giác QPM có:
MN = QP (gt)
NQ = PM (gt)
MQ cạnh chung
Vậy ΔMNQ = ΔQPM (c.c.c)
- Hình 70
Xét tam giác EHI và tam giác IKE có:
EH = IK (gt)
HI = KE (gt)
EI = IE (cạnh chung)
Vậy ΔEHI = ΔIKE (c.c.c)
Xét tam giác EHK và tam giác IKH có:
EH = IK (gt)
EK = IH (gt)
HK = KH (cạnh chung)
Vậy ΔEHK = ΔIKH (c.c.c)
BÀI 18 :
1) Ghi giả thiết và kết luận:
2) Thứ tự sắp xếp là d-b-a-c
ΔAMN và Δ BMN có:
MN: cạnh chung
MA = MB (gt)
NA = NB (gt)
Do đó Δ MNA = ΔBMN (c.c.c)
Bài 19 :
a) ΔADE và ΔBDE có:
DE cạnh chung
AD = BD (gt)
AE = BE (gt)
Vậy ΔADE = ΔBDE (c.c.c)
b) Từ ΔADE = ΔBDE (cmt) suy ra
Bài 20 :
Nối BC, AC
ΔOBC và ΔOAC có:
OB = OA (bán kính)
AC = BC (gt)
OC cạnh chung
Nên ΔOBC = ΔOAC (c.c.c)
Bài 21 :
Lời giải:
- Vẽ phân giác của góc A
+Vẽ cung tròn tâm A cung này cắt AB, AC theo thứ tự ở M, N.
+Vẽ các cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau ở điểm I nằm trong góc BAC
+Nối AI, ta được AI là tia phân giác của góc A.
- Tương tự cho cách vẽ tia phân giác của góc B, C
Bài 15:
-Vẽ đoạn MN=2,5cmMN=2,5cm
- Trên cùng một nửa mặt phẳng bờ MNMN vẽ cung tròn tâm MM bán kính 5cm5cm và cung tròn tâm NN bán kinh 3cm3cm.
- Hai cung tròn cắt nhau tại PP. Vẽ các đoạn MN,NPMN,NP, ta được tam giác MNPMNP.
bài 16:
Vẽ tam giác ABC tương tự như hinh vẽ ở bài 15.
Đo mỗi góc của tam giác ABC ta được:
ˆAA^=ˆBB^=ˆCC^= 600
Bài 17
Hình a.
Ta có: AB=AB(cạnh chung)
AC= AD(gt)
BC=BD(gt)
vậy ∆ABC= ∆ABD(c.c.c)
* Hình b.
Ta có:
∆MNQ=∆QPM(c.c.c)
vì MN=QP(gt)
NQ=PM(gt)
MQ=QM(cạnh chung)
* Hình c.
Ta có:
∆EHI=∆IKE(c.c.c) vì
EH=IK(gt)
HI=KE(gt)
EI=IE(gt)
+ ∆EHK=∆IKH(c.c.c) vì
EH=IK(gt)
EK=IH(gt)
HK=KH(cạnh chung)
Bài 18:

2) sắp xếp theo thư tự.
d,b,a,c.
Bài 19:
Xem hình vẽ:
a) ∆ADE và ∆BDE có
DE cạnh chung
AD=DB(gt)
AE=BE(gt)
Vậy ∆ADE=∆BDE(c.c.c)
b) Từ ∆ADE=∆BDE(cmt)
Suy ra ˆDAE=ˆDBEDAE^=DBE^(Hai góc tương ứng)
Bài 20:
Vẽ cung tròn tâm OO, cung tròn này cắt Ox,OyOx,Oy theo thứ tự ở A,BA,B do đó OA=OBOA=OB vì cùng bằng bán kính của cung tròn
Cung tròn tâm AA và tâm BB có cùng bán kính nên ta gọi bán kính là rr
CC là giao của hai cung tròn do đó CC thuộc cung tròn tâm AA nên AC=rAC=r, CC thuộc cung tròn tâm BB nên BC=rBC=r
Suy ra AC=BCAC=BC
Nối BC,ACBC,AC.
Xét ΔOBC∆OBC và ΔOAC∆OAC có:
+) OB=OAOB=OA
+) BC=ACBC=AC
+) OCOC cạnh chung
Suy ra ΔOBC=ΔOAC(c.c.c)∆OBC=∆OAC(c.c.c)
Nên ˆBOC=ˆAOCBOC^=AOC^ (hai góc tương ứng)
Vậy OCOC là tia phân giác của góc xOyxOy.
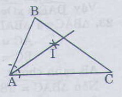
Bài 21:
Vẽ tia phân giác của góc A.
Vẽ cung trong tâm A, cung tròn này cắt AB, AC theo thứ tự ở M,N.
Vẽ các cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau ở điểm I nằm trong góc BAC.
Nối AI, ta được AI là tia phân giác của góc A.
Tương tự cho cách vẽ tia phân giác của các góc B,C(Học sinh tự vẽ)
Bạn hỏi nhiều thế này sao mình làm nổi !!! ![]()
![]()
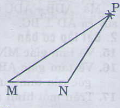
15. ΔMNP, biết MN=2,5 cm, NP=3cm, PM= 5cm,
Các bước lần lượt như sau:
– Dùng thước vẽ đoạn MN = 2,5cm
– Trên cùng một nửa mặt phẳng bở MN, dùng Compa vẽ cung tròn tâm M bán kính 5cm và cung tròn tâm N bán kinh 3cm.
– Hai cung tròn cắt nhau tại P. Vẽ các đoạn MN, NP, ta được ΔMNP (hình vẽ).
16.Vẽ tam giác biết độ dài mỗi cạnh là 3 cm. Sau đó đo góc của mỗi tam giác.

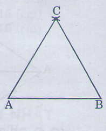
Cách vẽ ΔABC tương tự như cách vẽ ở bài15 (Phía trên).
Đo mỗi góc của ΔABC ta được: ∠A = ∠B = ∠C =600
17. Trên mỗi hình 68,69,70 sau có tam giác nào bằng nhau? Vì sao?
* Hình 68: Ta có: AB = AB(cạnh chung)
AC = AD (gt)
BC = BD (gt)
vậy ∆ABC= ∆ABD(c.c.c)
* Hình 69. Ta có:
∆ MNQ = ∆ QPM (c.c.c)
vì MN = QP (gt)
NQ = PM(gt)
MQ = QM(cạnh chung)
* Hình 70. Ta có:
∆ EHI = ∆IKE (c.c.c) vì
EH = IK (gt)
HI = KE (gt)
EI = IE(gt)
∆ EHK= ∆ IKH(c.c.c) vì
EH = IK (gt)
EK = IH (gt)
HK = KH (cạnh chung)
Luyện tập 1: Giải bài 18, 19, 20, 21 Toán 7 tập 1
18. Xét bàitoán: “Δ AMB và Δ ANB có MA = MB, NA = NB (h.71). Chứng minh rằng:∠AMN = ∠BMN.”
Xét bàitoán: “Δ AMB và Δ ANB có MA = MB, NA = NB (h.71). Chứng minh rằng:∠AMN = ∠BMN.”
1) Hãy ghi giả thiết và kết luận
2) Hãy sắp xếp bốn câu sau đây một cách hợp lý để giải bàitoán trên :
a) Do đó Δ AMN= Δ BMN(c.c.c)
b) MN: cạnh chung
MA= MB( Giả thiết)
NA= NB( Giả thiết)
c) Suy ra ∠AMN = ∠BMN (2 góc tương ứng)
d)Δ AMB và Δ ANB có:
HD: 1)Ghi Giả thiết, kết luận:
 2) sắp xếp theo thư tự: d,b,a,c.
2) sắp xếp theo thư tự: d,b,a,c.
Bài 19. Cho hình 72. Chứng minh rằng:
Cho hình 72. Chứng minh rằng:
a) ∆ADE = ∆BDE.
b) ∠ADE = ∠DBE.
Xem hình vẽ ta có:
a) ∆ADE và ∆BDE có:
DE cạnh chung
AD = DB (gt)
AE = BE(gt)
Vậy ∆ADE = ∆BDE(c.c.c)
b) Từ ∆ADE = ∆BDE(Cmt) (Giải thích “cmt”: chứng minh trên)
Suy ra ∠ADE = ∠DBE (Hai góc tương ứng 2 Δ = nhau)
Bài 20 Toán 7. Cho ∠xOy (h.73), Vẽ cung tròn tâm O, cung tròn này cắt Ox, Oy theo thứ tự ở A,B (1). Vẽ các cung tròn tâm A và tâm B có cùng bán kính sao cho chúng cắt nhau ở điểm C nằm trong ∠xOy ((2) (3)). Nối O với C (4). Chứng minh OC là tia phân giác của ∠xOy.
Cho ∠xOy (h.73), Vẽ cung tròn tâm O, cung tròn này cắt Ox, Oy theo thứ tự ở A,B (1). Vẽ các cung tròn tâm A và tâm B có cùng bán kính sao cho chúng cắt nhau ở điểm C nằm trong ∠xOy ((2) (3)). Nối O với C (4). Chứng minh OC là tia phân giác của ∠xOy.
HD. xem hình vẽ:
Nối BC, AC.
∆OBC và ∆OAC có:
OB = OA(Bán kính)
BC = AC(gt)
OC cạnh chung
nên ∆OBC = ∆OAC (c.c.c)
Nên ta có ∠BOC = ∠AOC (hai góc tương ứng)
Vậy OC là tia phân giác xOy.
21. Cho ΔABC, Dùng thước và compa, vẽ các tia phân giác của các ∠A,∠B,∠C.
Vẽ tia phân giác của ∠A.
Vẽ cung trong tâm A, cung tròn này cắt AB, AC theo thứ tự ở M,N.
Vẽ các cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau ở điểm I nằm trong ∠BAC.
Nối AI, ta được AI là tia phân giác của ∠A.
Tương tự cho cách vẽ tia phân giác của các ∠B,∠C (Học sinh tự vẽ).
haha dài lắm ko có chuyện ngồi đấy nhờ cầu cứu đâu
ai thương tiếc lắm thì giúp cậu đó ''Thảo Nguyên''