ta có : góc CAB=1/2 sđ cung CB
góc CDB = 1/2 sđ cung CB
-> góc CAB= góc CDB
ta lại có : góc ACD =1/2 sđ cung AD
góc ABD =1/2 sđ cung AD
-> góc ACD = góc ABD
xét tam giác EAC và EDB có;
góc EAC=góc EDB( CMT)
góc ACE= góc DBE(cmt)
-> 2 tam giác đồng dạng theo trường hợp g.g
-> EA/EC=ED/EB
-> EA.EB=EC.ED
Từ một điểm A ở bên ngoài đường tròn (O), vẽ tiếp tuyến AB và cát tuyến ACD với đường tròn (B là tiếp điểm, C nằm giữa A và D). Tia phân giác của góc CBD cắt đường tròn tại m, cắt CD tại E và cắt tia phân giác của góc BAC tại H. Chứng minh rằng:
a) AH ⊥ BE
b) MD2=MB.ME
Các bạn giúp mik vs ạ
Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh tam giác AEH là tam giác cân.
Trên đường tròn (O; R) vẽ ba dây liên tiếp bằng nhau. AB, BC, CD mỗi dây có độ dài nhỏ hơn R. Các đường thẳng AB và CD cắt nhau tại I, các tiếp tuyến của đường tròn tại B, D cắt nhau tại K
a) Chứng minh \(\widehat{BIC}=\widehat{BKD}\)
b) Chứng minh BC là tia phân giác của \(\widehat{KBD}\)
Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên trong đường tròn. Chứng minh \(\widehat{A}+\widehat{BSM}=2.\widehat{CMN}.\)
Hai dây cung AB và CD kéo dài cắt nhau tại điểm E ở ngoài đường tròn (O) (B nằm giữa A và E, C nằm giữa D và E). Cho biết \(\widehat{CBE}=75^0,\widehat{CEB}=22^0,\widehat{AOD}=144^0\)
Chứng minh :
\(\widehat{AOB}=\widehat{BAC}\)
Qua điểm M nằm bên ngoài đường tròn (O), vẽ tiếp tuyến AB và cát tuyến MAB của đường tròn . Tia phân giác của góc ACB cắt dây AB tại I. Chứng minh MC=MI
Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao cho 
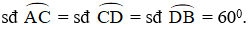Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:
Cho AB và CD là hai đường kính vuông góc của đường tròn (O). Trên cung nhỏ BD lấy một điểm M. Tiếp tuyến tại M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S. Chứng minh ES = EM.