Question

1) Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.

2) Hình thang ABCD có đáy AB, CD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, BD. Chứng minh ba điểm E, K, F thẳng hàng.

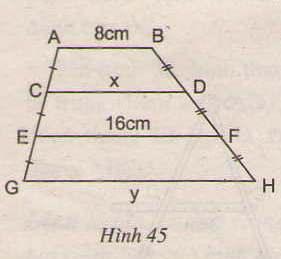
3) Tính x, y trên hình 45, trong đó AB // CD // EF // GH.

Giải chi tiết nha các bạn

Answer 1

1)Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.

Bài giải:

Kẻ AH, CM, BK vuông góc với xy (H, M, K là chân đường vuông góc).

Hình thang ABKH có AC = CB,

CM // AH // BK

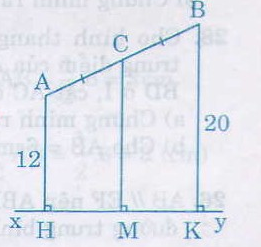
nên MH = MK và CM là đường trung bình.

Do đó

2)Hình thang ABCD có đáy AB, CD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, BD. Chứng minh ba điểm E, K, F thẳng hàng.

Bài giải:

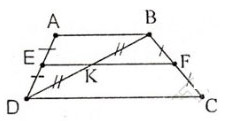
Ta có EA = ED, KB = KD (gt)

Nên EK // AB

Lại có FB = FC, KB = KD (gt)

Nên KF // DC // AB

Qua K ta có KE và KF cùng song song với AB nên theo tiên đề Ơclit ba điểm E, K, F thẳng hàng.

3)Tính x, y trên hình 45, trong đó AB // CD // EF // GH.

Bài giải:

AB // EF nên ABFE là hình thang CA = CE và DB = DF nên CD là đường trung bình của hình thang ABFE.

Do đó: CD = = = 12

Hay x = 12

Tương tự CDHG là hình thang, EF là đường trung bình của hình thang CDHG.

Nên EF = => GH = 2EF -CD = 2.16 - 12

GH = 20 hay y = 20

Vậy x = 12, y = 20