Bài giải:
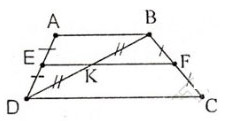
Ta có EA = ED, KB = KD (gt)
Nên EK // AB
Lại có FB = FC, KB = KD (gt)
Nên KF // DC // AB
Qua K ta có KE và KF cùng song song với AB nên theo tiên đề Ơclit ba điểm E, K, F thẳng hàng.
\(\Delta ADB\) có:\(AE=DE\left(gt\right),BF=FD\left(gt\right)\)
\(\Rightarrow AB\) // \(EF\)(theo đlí 2 về đường trung bình của tam giác) (1)
\(\Delta BDC\) có:\(BK=KC\left(gt\right),BF=FD\left(gt\right)\)
\(\Rightarrow FK\) // \(CD\)(theo đlí 2 về đường trung bình của tam giác)
Mà \(CD\) // \(AB\Rightarrow FK\) // \(AB\) (1)
Từ (1) và (2), suy ra:
\(AB\) // \(EF,FK\)
\(\Rightarrow E,F,K\) thẳng hàng (theo tiên đề Ơclit )
tham khảo bài mk nha!
Vì E là trung điểm của AD và BC => EF là đường trung bình của hình thang ABCD => EF//AB//CD
Do E và K là trung điểm của AD và BD => EK là đường trung bình của tam giác ABD => EK//AB
Do F và K là trung điểm của BC và BD => FK là đường trung bình của tam giác BCD => FK//BC
Mà AB//CD => EF;EK;FK cùng song song với AB => E,F,K thẳng hàng.


