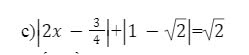Ta có: \(\left|2x-\dfrac{3}{4}\right|+\left|1-\sqrt{2}\right|=\sqrt{2}\)
=>\(\left|2x-\dfrac{3}{4}\right|+\sqrt{2}-1=\sqrt{2}\)
=>\(\left|2x-\dfrac{3}{4}\right|=1\)
=>\(\left[{}\begin{matrix}2x-\dfrac{3}{4}=1\\2x-\dfrac{3}{4}=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=1+\dfrac{3}{4}=\dfrac{7}{4}\\2x=-1+\dfrac{3}{4}=-\dfrac{1}{4}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{7}{4}:2=\dfrac{7}{8}\\x=-\dfrac{1}{4}:2=-\dfrac{1}{8}\end{matrix}\right.\)
\(\left|2x-\dfrac{3}{4}\right|+\left|1-\sqrt{2}\right|=\sqrt{2}\)
\(=>\left|2x-\dfrac{3}{4}\right|+\sqrt{2}-1=\sqrt{2}\) (vì \(1-\sqrt{2}< 0\))
\(=>\left|2x-\dfrac{3}{4}\right|=\sqrt{2}-\sqrt{2}+1\)
`=> |2x - 3/4| = 1`
TH1: 2x - 3/4 = 1`
`=> 2x = 1 + 3/4`
`=> 2x = 7/4`
`=> x = 7/4 : 2`
`=> x =7/8`
TH2:
`2x - 3/4 =-1`
`=> 2x = -1 +3/4`
`=> 2x = -1/4`
`=> x = -1/4 : 2`
`=> x= -1/8`
Vậy ...