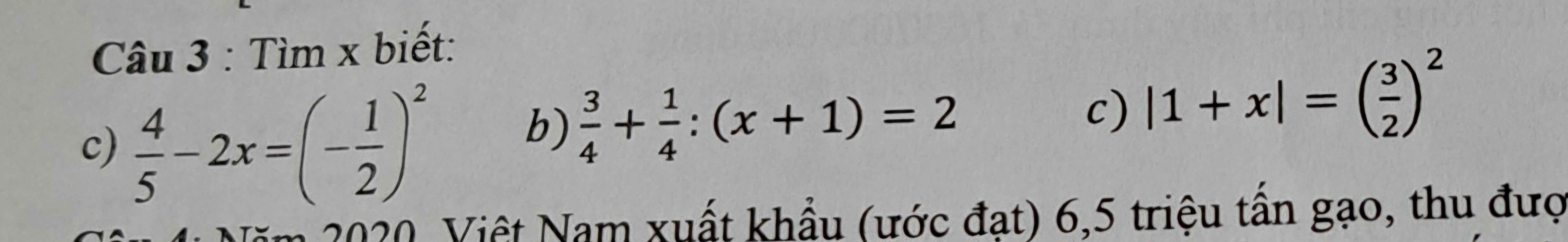Câu 3:
\(c,\dfrac{4}{5}-2x=\left(-\dfrac{1}{2}\right)^2\)
\(2x=\dfrac{4}{5}-\left(-\dfrac{1}{2}\right)^2\)
\(2x=\dfrac{4}{5}-\dfrac{1}{4}\)
\(2x=\dfrac{16}{20}-\dfrac{5}{20}\)
\(2x=\dfrac{11}{20}\)
\(x=\dfrac{11}{20}:2\)
\(x=\dfrac{11}{20}.\dfrac{1}{2}\)
\(x=\dfrac{11}{40}\)
Vậy ...
\(d,\dfrac{3}{4}+\dfrac{1}{4}:\left(x+1\right)=2\)
\(\dfrac{1}{4}:\left(x+1\right)=2-\dfrac{3}{4}\)
\(\dfrac{1}{4}:\left(x+1\right)=\dfrac{8}{4}-\dfrac{3}{4}\)
\(\dfrac{1}{4}:\left(x+1\right)=\dfrac{5}{4}\)
\(x+1=\dfrac{1}{4}:\dfrac{5}{4}\)
\(x+1=\dfrac{1}{4}.\dfrac{4}{5}\)
\(x+1=\dfrac{1}{5}\)
\(x=\dfrac{1}{5}-1\)
\(x=\dfrac{-4}{5}\)
Vậy ...
\(c,\left|1+x\right|=\left(\dfrac{3}{2}\right)^2\)
\(\left|1+x\right|=\dfrac{9}{4}\)
\(1+x=\dfrac{9}{4}\) hoặc \(1+x=\dfrac{-9}{4}\)
\(x=\dfrac{9}{4}-1\) \(x=\dfrac{-9}{4}-1\)
\(x=\dfrac{5}{4}\) \(x=\dfrac{-13}{4}\)
Vậy ...
a: \(\dfrac{4}{5}-2x=\left(-\dfrac{1}{2}\right)^2\)
=>\(\dfrac{4}{5}-2x=\dfrac{1}{4}\)
=>\(2x=\dfrac{4}{5}-\dfrac{1}{4}=\dfrac{11}{20}\)
=>\(x=\dfrac{11}{40}\)
b: \(\dfrac{3}{4}+\dfrac{1}{4}:\left(x+1\right)=2\)
=>\(\dfrac{1}{4}:\left(x+1\right)=2-\dfrac{3}{4}=\dfrac{5}{4}\)
=>\(x+1=\dfrac{1}{4}:\dfrac{5}{4}=\dfrac{1}{5}\)
=>\(x=\dfrac{1}{5}-1=-\dfrac{4}{5}\)
c: \(\left|1+x\right|=\left(\dfrac{3}{2}\right)^2\)
=>\(\left|x+1\right|=\dfrac{9}{4}\)
=>\(\left[{}\begin{matrix}x+1=\dfrac{9}{4}\\x+1=-\dfrac{9}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{4}\\x=-\dfrac{9}{4}-1=-\dfrac{13}{4}\end{matrix}\right.\)