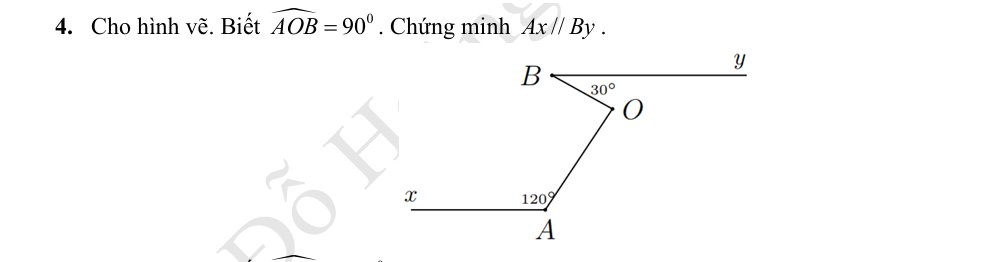
Qua O, kẻ tia OC nằm giữa hai tia OA và OB sao cho OC//By
Ta có: OC//By
=>\(\widehat{COB}=\widehat{yBO}\)(hai góc so le trong)
=>\(\widehat{COB}=30^0\)
Ta có: tia OC nằm giữa hai tia OA và OB
=>\(\widehat{COA}+\widehat{COB}=\widehat{AOB}\)
=>\(\widehat{COA}=90^0-30^0=60^0\)
Ta có: \(\widehat{COA}+\widehat{xAO}=120^0+60^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên OC//Ax
mà OC//By
nên Ax//By
kẻ `Oz` // `Ax` :
`=>`\(\widehat{xAO}+\widehat{zOA}=180^0\)(2 góc trong cùng phía)
`=>`\(\widehat{zOA}=180^0-130^0=50^0\)
Lại có : \(\widehat{BOz}+\widehat{zOA}=\widehat{BOA}\)
Mà \(\widehat{BOA}=90^0\)
`=>`\(\widehat{BOz}+50^0=90^0\)
`=>`\(\widehat{BOz}=90^0-50^0=30^0\)
Vì : \(\widehat{zOB}=\widehat{OBy}=30^0\)
Mà 2 góc ở vị trí so le trong
`=>zO` // `By`
Có :`zO` // `Ax`
`=> Ax` // `By`