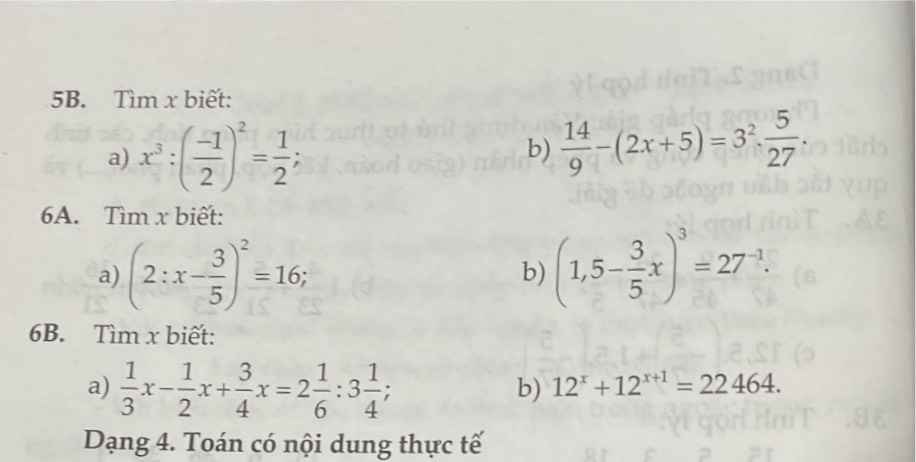`1`
`x^3 : (-1/2)^2 = 1/2`
`=> x^3 : (1/2)^2 = 1/2`
`=> x^3 = (1/2)^3`
`=> x = 1/2`
Vậy `x = 1/2`
`14/9 - (2x + 5) = 3^2 . 5/27`
`=> 14/9 - 2x - 5 = 9 . 5/27`
`=> -31/9 - 2x = 5/3`
`=> -2x = 5/3 + 31/9 = 46/9`
`=> x = -23/9`
Vậy `x = -23/9`
`2`
(2:x - 3/2)^2= 16`
`TH1: 2:x - 3/2 = 4`
`=> 2 : x = 11/2`
`=> x = 4/11`
`TH2: 2 : x - 3/2 = -4`
`=> 2 : x =-5/2`
`=> x = -4/5`
Vậy `x ∈{4/11 ; -4/5}`
`(1,5 - 3/5x)^3 = 27^(-1)
`=> (1,5 - 3/5x)^3 = 1/27`
`=> 1,5 - 3/5x = 1/3`
`=> 3/5x = 7/6`
`=> x = 35/18`
Vậy `x = 35/18`
`3`
`1/3x - 1/2x +3/4x = 2 1/6 : 3 1/4`
`= (1/3 - 1/2 + 3/4)x = 2/3`
`=> 7/12 x = 2/3`
`=> x = 8/7`
Vậy `x = 8/7`
`12^x + 12^(x+1) = 22464`
`=> 12^x + 12^x . 12 = 22464`
`=> 12^x(1 + 12) = 22464`
`=> 12^x = 1728`
`=> 12^x = 12^3`
`=> x = 3`
Vậy `x = 3`
5B.
\(a,x:\left(\dfrac{-1}{2}\right)^2=\dfrac{1}{2}\)
\(x=\dfrac{1}{2}.\left(\dfrac{-1}{2}\right)^2\)
\(x=\dfrac{1}{2}.\dfrac{1}{4}\)
\(x=\dfrac{1}{8}\)
Vậy \(x=\dfrac{1}{8}\)
\(b,\dfrac{14}{9}-\left(2x+5\right)=3^2.\dfrac{5}{27}\)
\(\dfrac{14}{9}-\left(2x+5\right)=9.\dfrac{5}{27}\)
\(\dfrac{14}{9}-\left(2x+5\right)=\dfrac{5}{3}\)
\(2x+5=\dfrac{14}{9}-\dfrac{5}{3}\)
\(2x+5=\dfrac{14}{9}-\dfrac{15}{9}\)
\(2x+5=\dfrac{-1}{9}\)
\(2x=\dfrac{-1}{9}-5\)
\(2x=\dfrac{-1}{9}-\dfrac{45}{9}\)
\(2x=\dfrac{-46}{9}\)
\(x=\dfrac{-46}{9}:2\)
\(x=\dfrac{-46}{9}.\dfrac{1}{2}\)
\(x=\dfrac{-23}{9}\)
Vậy \(x=\dfrac{-23}{9}\)
Mình làm lại ý a câu 5B ạ
\(a,x^3:\left(\dfrac{-1}{2}\right)^2=\dfrac{1}{2}\)
\(x^3=\dfrac{1}{2}.\left(\dfrac{-1}{2}\right)^2\)
\(x^3=\dfrac{1}{2}.\dfrac{1}{4}\)
\(x^3=\dfrac{1}{8}\)
\(x^3=\dfrac{1}{2^3}\)
\(x^3=\left(\dfrac{1}{2}\right)^3\)
\(x=\dfrac{1}{2}\)
Vậy \(x=\dfrac{1}{2}\)