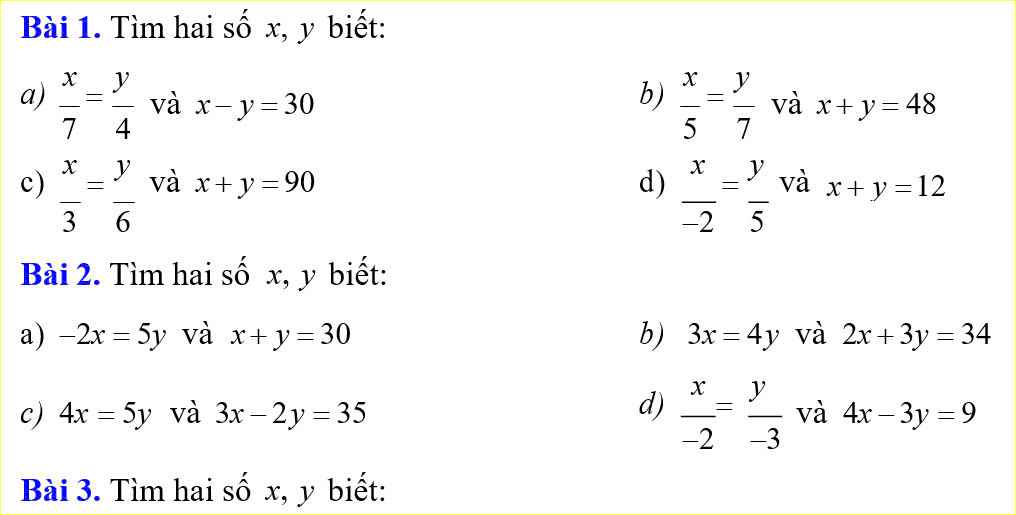a) Áp dụng t/chất dãy tỉ số bằng nhau:
`=> x/7 = y/4 = (x-y)/(7-4) = 30/3 = 10`
`=> {(x/7 = 10 => x = 70),(y/4 = 10 => y = 40):} `
Vậy ...
b) Áp dụng t/chất dãy tỉ số bằng nhau:
`x/5 = y/7 = (x+y)/(5+7) = 48/12 = 4 `
`=> {(x/5 = 4 => x = 20),(y/7 = 4 => y = 28):} `
Vậy ...
c, \(\dfrac{x}{3}=\dfrac{y}{6}\) và \(x+y=90\)
\(\Rightarrow\dfrac{x}{3}=\dfrac{y}{6}=\dfrac{x+y}{3+6}=\dfrac{90}{9}=10\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=10\Rightarrow x=30\\\dfrac{y}{6}=10\Rightarrow x=60\end{matrix}\right.\)
Vậy .....
c) Áp dụng t/chất dãy tỉ số bằng nhau:
`x/3 = y/6 = (x+y)/(3+6) = 90/9 = 10`
`=> {(x/3= 10=> x = 30),(y/6 = 10 => y=60):}`
Vậy ...
d) Áp dụng t/chất dãy tỉ số bằng nhau:
`x/(-2) = y/(-3) = (4x - 3y)/((-2).4 - 3(-3)) = 9/1 = 9`
`=> {(x/(-2) = 9 => x = -18),(y/(-3) = 9 => y = -27):}`
Vậy ...
Bài 2:
a: -2x=5y
=>\(\dfrac{x}{5}=\dfrac{y}{-2}\)
mà x+y=30
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{5}=\dfrac{y}{-2}=\dfrac{x+y}{5-2}=\dfrac{30}{3}=10\)
=>\(x=5\cdot10=50;y=-2\cdot10=-20\)
b: 3x=4y
=>\(\dfrac{x}{4}=\dfrac{y}{3}=k\)
=>x=4k; y=3k
2x+3y=34
=>\(2\cdot4k+3\cdot3k=34\)
=>8k+9k=34
=>17k=34
=>k=2
=>\(x=4\cdot2=8;y=3\cdot2=6\)
c: 4x=5y
=>\(\dfrac{x}{5}=\dfrac{y}{4}=k\)
=>x=5k; y=4k
3x-2y=35
=>\(3\cdot5k-2\cdot4k=35\)
=>15k-8k=35
=>7k=35
=>k=5
=>\(x=5\cdot5=25;y=4\cdot5=20\)
d: Ta có: \(\dfrac{x}{-2}=\dfrac{y}{-3}\)
=>\(\dfrac{x}{2}=\dfrac{y}{3}=k\)
=>x=2k; y=3k
4x-3y=9
=>\(4\cdot2k-3\cdot3k=9\)
=>8k-9k=9
=>-k=9
=>k=-9
=>\(x=2\cdot\left(-9\right)=-18;y=3\cdot\left(-9\right)=-27\)